Ordinary least squares (OLS) hay Bình phương nhỏ nhất là phương pháp hồi quy nhằm tìm được đường thẳng tốt nhất để mô tả mối liên hệ tuyến tính giữa biến độc lập và biến phụ thuộc.
OLS giúp ước lượng phương trình hồi quy sau:
ŷ = b0 + b1x
Trong đó:
- ŷ: Biến phụ thuộc theo lý thuyết
- b0: Hệ số gốc
- b1: Hệ số góc
Bước 1: Tạo dữ liệu
Tạo dataset có 2 biến với 15 quan sát như sau:
- Chi phí quảng cáo
- Doanh thu
Lưu ý: 15 quan sát này trong thực tế là không đủ tin cậy để ước lượng hồi quy, tuy nhiên vì là ví dụ nên ta chấp nhận quy mô bộ dữ liệu này.
Thực hiện hồi quy OLS, với chi phí quảng cáo là biến độc lập, doanh thu là biến phụ thuộc:
1#create dataset
2chi_phi_quang_cao <- c(10, 15, 20, 25, 30, 35, 40, 45, 50, 55)
3doanh_thu <- c(100, 120, 150, 180, 210, 240, 260, 265, 267, 280)
4df <- data.frame(chi_phi_quang_cao, doanh_thu)
5
6#view dataset
7View(df)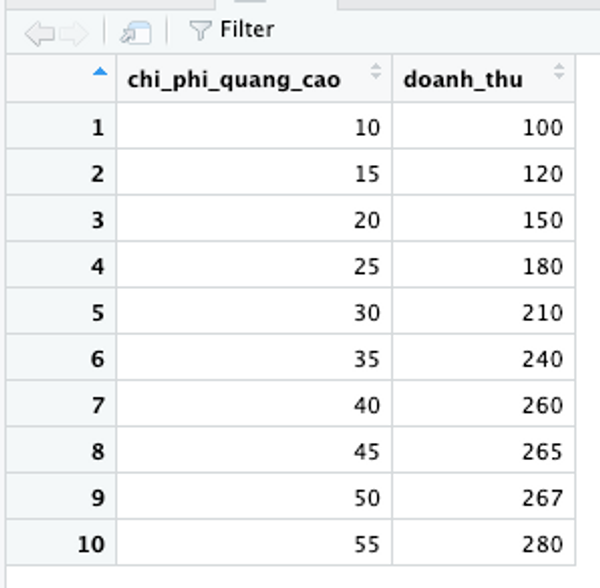
Bước 2: Trực quan hoá
1library(ggplot2)
2
3#create scatter plot
4ggplot(df, aes(x=chi_phi_quang_cao, y=doanh_thu)) +
5 geom_point(size=2)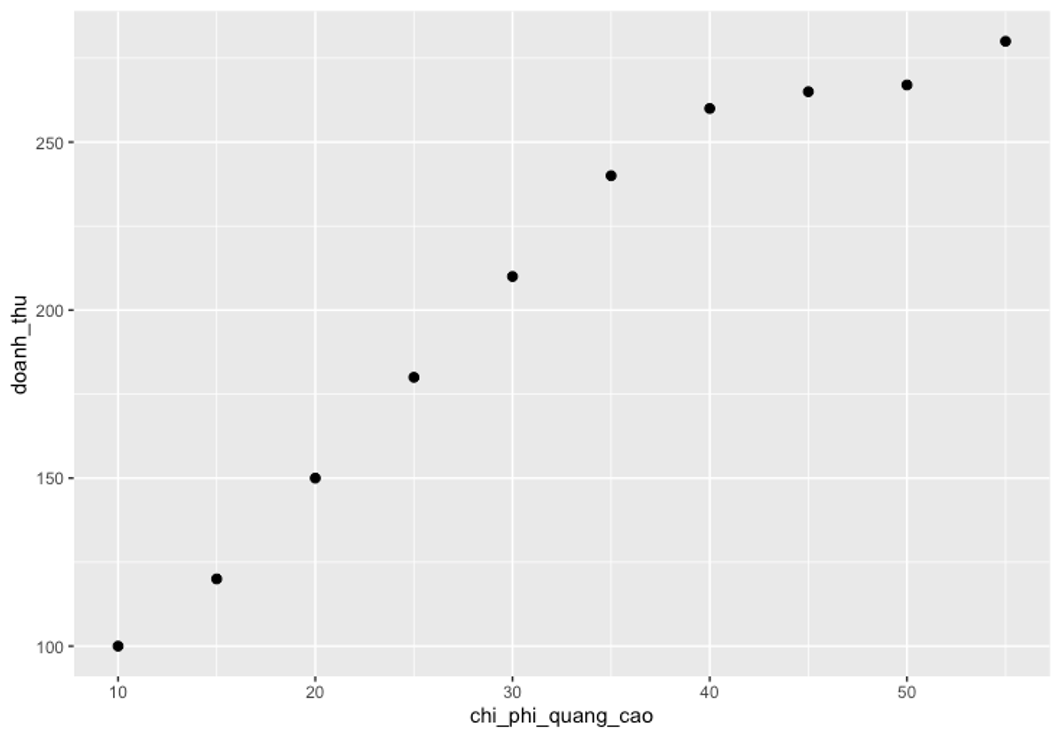
Một trong các giả định của hồi quy tuyến tính là có mối liên hệ tuyến tính giữa biến độc lập và biến phụ thuộc.
Từ biểu đồ có thể thấy mối liên hệ như sau: khi chi phí quảng cáo tăng, doanh thu cũng tăng tuyến tính theo.
Tiếp theo, ta có thể dùng boxplot để trực quan hóa phân phối doanh thu và kiểm tra các outliers.
Lưu ý: R xác định một quan sát là outlier nếu nó lớn hơn 1,5 lần tính từ phân vị mức 75 của phân phối hoặc nhỏ hơn 1,5 lần tính từ phân vị mức 25.
Nếu một quan sát là outlier, một vòng tròn nhỏ sẽ xuất hiện trong boxplot:
1library(ggplot2)
2
3#create scatter plot
4ggplot(df, aes(y=score)) +
5 geom_boxplot()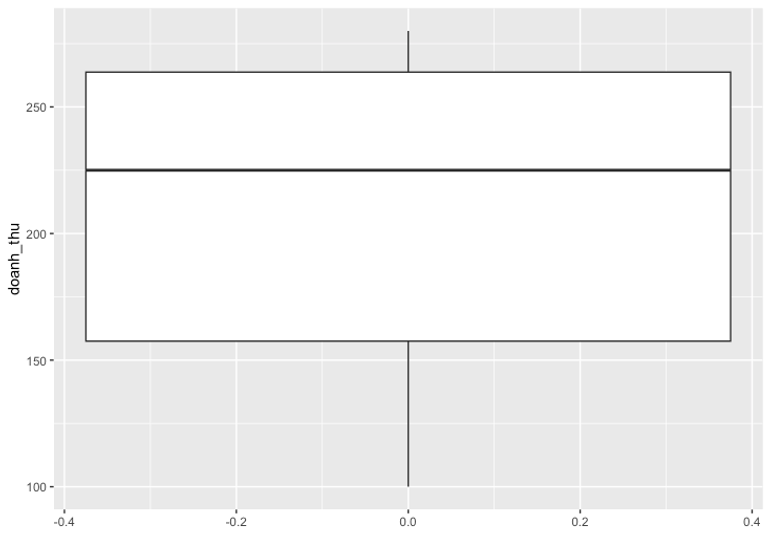
Không có vòng tròn nhỏ nào ở hai đầu boxplot, điều đó có nghĩa là không có giá trị outliers nào trong dataset này.
Bước 3: Thực hiện hồi quy OLS
Sử dụng hàm lm() trong R để thực hiện hồi quy OLS, sử dụng chi_phi_quang_cao làm biến độc lập và doanh_thu làm biến phụ thuộc:
1#fit simple linear regression model
2m1 <- lm(doanh_thu~chi_phi_quang_cao, data=df)
3
4#view model summary
5summary(m1)Kết quả thu được
1Call:
2lm(formula = doanh_thu ~ chi_phi_quang_cao, data = df)
3
4Residuals:
5 Min 1Q Median 3Q Max
6-22.4909 -12.7909 0.1515 11.2561 22.2121
7
8Coefficients:
9 Estimate Std. Error t value Pr(>|t|)
10(Intercept) 69.5576 12.9789 5.359 0.000678 ***
11chi_phi_quang_cao 4.2352 0.3653 11.594 2.78e-06 ***
12---
13Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
14
15Residual standard error: 16.59 on 8 degrees of freedom
16Multiple R-squared: 0.9438, Adjusted R-squared: 0.9368
17F-statistic: 134.4 on 1 and 8 DF, p-value: 2.785e-06Từ model summary, có thể thấy phương trình hồi quy phù hợp là:
doanh_thu = 69.5576 + 4.2352(chi_phi_quang_cao)
Điều này có nghĩa là mỗi đồng chi phí quảng cáo tăng lên sẽ ảnh hưởng và làm tăng trung bình 4.2352 đồng doanh thu.
Hệ số gốc 69.5576 cho biết doanh thu trung bình dự kiến khi không có chi phí quảng cáo.
Ta cũng có thể sử dụng phương trình này để tìm doanh thu dự kiến dựa trên chi phí quảng cáo có được.
Ví dụ: nếu dùng 100 đồng chi phí quảng cáo thì doanh thu sẽ là:
doanh_thu = 69.5576 + 4.2352(100) = 493.0776
Đây là cách giải thích phần còn lại của model summary:
- Pr(>|t|): Đây là p-value của các hệ số của mô hình. Vì p-value cho chi phí quảng cáo (2.78e-06) nhỏ hơn đáng kể so với mức ý nghĩa 0,05 nên có thể kết luận rằng có mối liên hệ có ý nghĩa thống kê giữa chi phí quảng cáo và doanh thu.
- Multiple R-squared: cho biết tỷ lệ phần trăm biến thiên của biến phụ thuộc (doanh thu) có thể được giải thích bằng chi phí quảng cáo. Nhìn chung, giá trị bình phương R của mô hình hồi quy càng lớn thì các biến độc lập có khả năng dự đoán giá trị của biến phụ thuộc càng tốt. Trong trường hợp này, 94.38% sự thay đổi về doanh thu có thể được giải thích bằng chi phí quảng cáo.
- Residual standard error: Đây là khoảng cách trung bình mà các giá trị quan sát được nằm chệch khỏi đường hồi quy. Giá trị này càng thấp, đường hồi quy càng khớp với dữ liệu thực tế.
- F-statistic & p-value: Thống kê F (134.4) và giá trị p tương ứng (2.785e-06) cho biết ý nghĩa tổng thể của mô hình hồi quy, tức là liệu các biến độc lập trong mô hình có hữu ích để giải thích sự thay đổi trong biến phụ thuộc hay không. Vì p-value trong ví dụ này nhỏ hơn 0,05 nên mô hình của có ý nghĩa thống kê và chi phí quảng cáo được coi là hữu ích để giải thích sự thay đổi trong doanh thu.
Bước 4: Trực quan đường hồi quy
1ggplot(df, aes(x=chi_phi_quang_cao, y=doanh_thu)) +
2 geom_point(size=2) +
3 geom_smooth(method = "lm", se = F)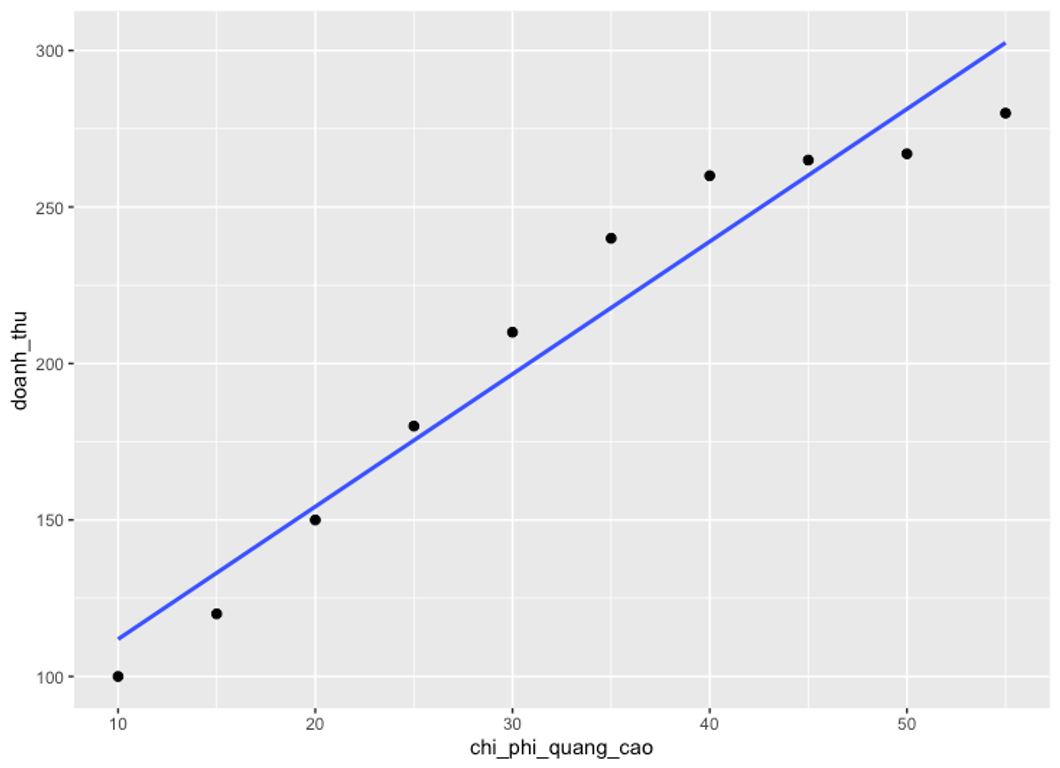
Bước 5: Residual Plots
Cuối cùng, ta cần vẽ các biểu đồ phân tích phần dư để kiểm tra các giả định về homoscedasticity và normality.
Giả định về homoscedasticity hay phương sai đồng nhất là phần dư của mô hình hồi quy có phương sai gần như bằng nhau ở mỗi cấp độ của một biến phụ thuộc.
Để kiểm tra giả định này, ta có thể tạo một biểu đồ phần dư so với giá trị fitted hay residuals vs. fitted plot.
Trục x hiển thị các giá trị fitted và trục y hiển thị phần dư. Nếu phần dư được phân phối ngẫu nhiên và đồng đều trong biểu đồ xung quanh giá trị 0, ta có thể giả định rằng homoscedasticity không bị vi phạm:
1#define residuals
2residuals <- resid(m1)
3
4#produce residual vs. fitted plot
5plot(fitted(m1), residuals)
6
7#add a horizontal line at 0
8abline(0,0)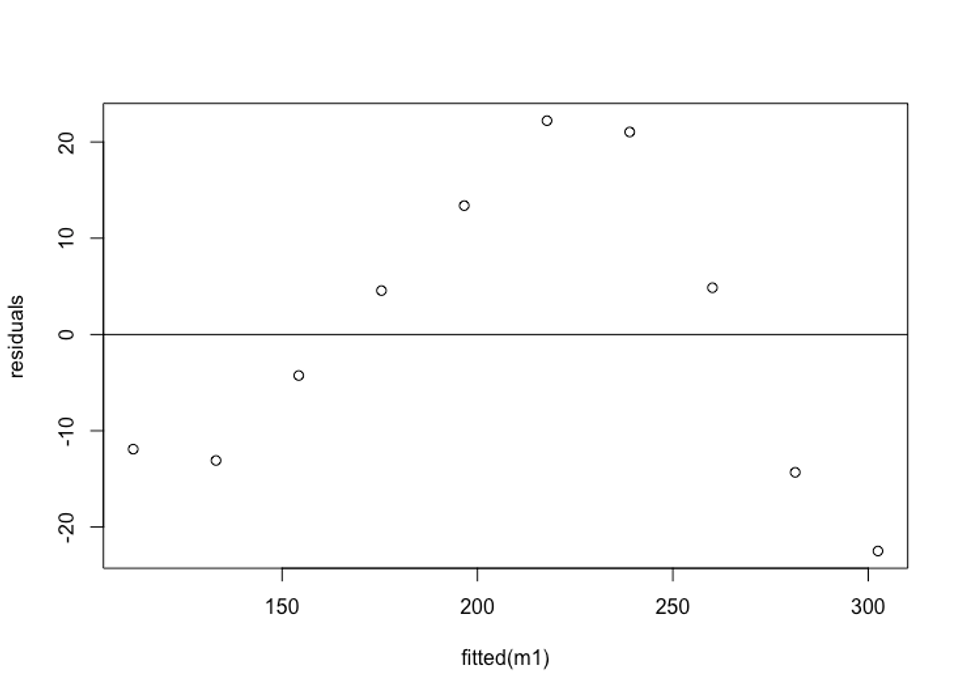
Phần dư gần như được rải ngẫu nhiên xung quanh 0 và không thể hiện bất kỳ patterns đáng chú ý nào, vì vậy giả định này được đáp ứng.
Giả định về normality chỉ ra rằng phần dư của một mô hình hồi quy gần như có phân phối chuẩn.
Để kiểm tra xem giả định này có được đáp ứng hay không, chúng ta có thể tạo biểu đồ Q-Q hay Q-Q plot. Nếu các điểm trong biểu đồ nằm dọc theo đường lý thuyết gần như thẳng ở góc 45 độ, thì dữ liệu được phân phối chuẩn:
1#create Q-Q plot for residuals
2qqnorm(residuals)
3
4#add a straight diagonal line to the plot
5qqline(residuals)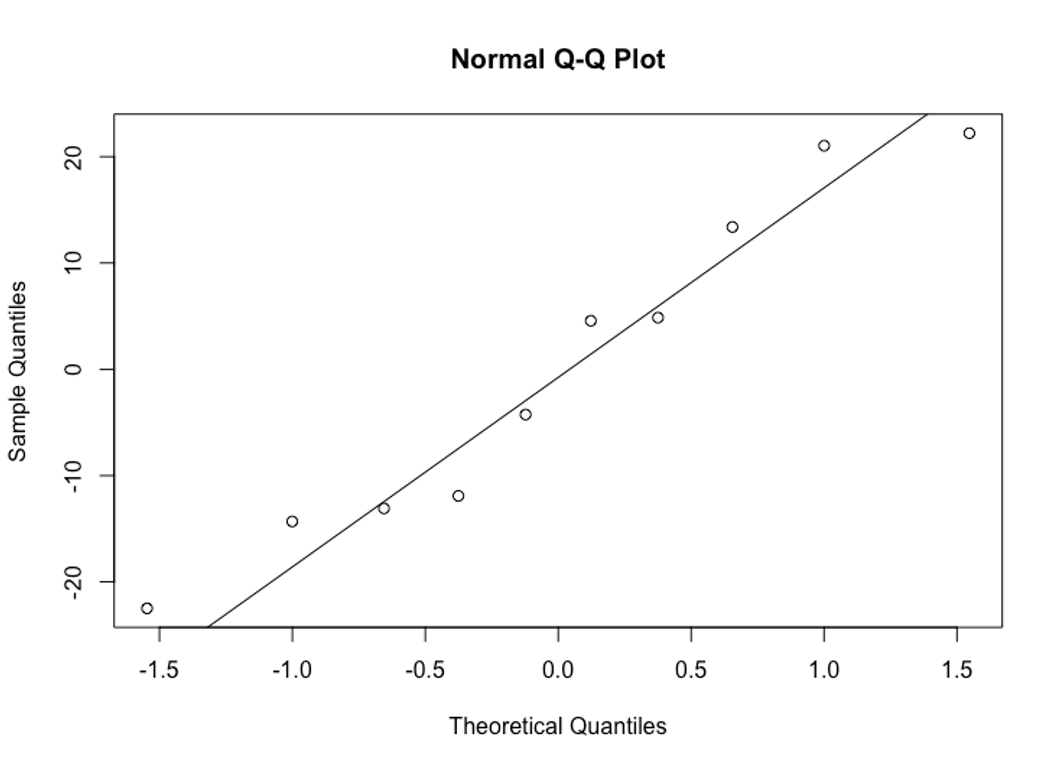
Ta thấy phần dư chệch khỏi đường 45 độ một chút, nhưng không đủ lớn. Chúng ta có thể kết luận rằng giả định được đáp ứng.
Vì phần dư được phân phối chuẩn và phương sai đồng nhất, ta đã xác minh rằng các giả định của mô hình hồi quy OLS được đáp ứng.
Do đó, đầu ra từ mô hình của này là đáng tin cậy.
Lưu ý: Nếu một hoặc nhiều giả định không được đáp ứng, ta có thể thử chuyển đổi dữ liệu.


