[BLOG 010] Thực hiện thuật toán phân cụm (K-means Clustering) với R

1. Giới thiệu

Phân cụm đồ thị (K-means Clustering) là quá trình phân chia hoặc tách biệt dữ liệu theo các nhóm dựa trên các đặc điểm chung sau đó được biểu thị qua một đồ thị. Phù hợp với những công việc cần phân khúc các tệp khách hàng trong thương mại, phân tích thị trường. Điều này giúp các công ty hiểu rõ hơn về sở thích và nhu cầu của từng nhóm, qua đó đưa ra chiến lược marketing phù hợp.

Trong thuật toán phân cụm, K-means là một thuật toán phân cụm đơn giản và phổ biến trong học máy (machine learning) để phân cụm các điểm dữ liệu thành các nhóm riêng biệt dựa trên các đặc điểm của chúng. Thuật toán này dùng để chia dữ liệu thành các nhóm dựa trên khoảng cách giữa các điểm dữ liệu với nhau.

2. Ta cài đặt những thư viện sau

1install.packages(c("ggplot2", "tidyverse","ICSNP","factoextra", "cluster"))

Thư viện ggplot2: Thực hiện vẽ biểu đồ cluster

Thư viện tidyverse: Cung cấp chức năng thao tác và biến đổi dữ liệu một cách trực quan

Thư viện factoextra: Thực hiện phân tích các kết quả từ các phương pháp phân tích đa chiều

Thư viện ICSNP: Thực hiện các phép kiểm định thống kê liên quan đến các phân phối đa biến

Thư viện cluster: Cung cấp các kiểm định chất lượng của số cụm

Sau khi cài đặt trong các gói thư viện, ta nhập các thư viện trên trong phiên làm việc hiện tại bằng lệnh:

1library(ggplot2)
2library(tidyverse)
3library(factoextra)
4library(ICSNP)
5library(cluster)

3. Nhập và xử lý data

Trong một doanh nghiệp, để xác định rõ khách hàng mục tiêu cho sản phẩm của mình, các doanh nghiệp có thể phân loại khách hàng theo thuật toán sau và xác định nhóm đối tượng sẵn sàng sử dụng dịch vụ của doanh nghiệp nhất.

Dữ liệu được lưu trong tệp CSV với đuôi Mall_Customers.csv. Để nhập dữ liệu vào R, ta dùng hàm read.csv. Tuy nhiên, đôi khi tên cột trong file khó nhớ khiến cho người phân tích gặp khó khăn trong việc phân tích giống như trong file này, sử dụng hàm rename sẽ giúp cho độc giả linh hoạt hơn trong việc gọi biến.

1# setwd( Đường dẫn tới thư mục lưu file của bạn)
2setwd("E:/PL working/C")
3list.files() #liệt kê toàn bộ file trong thư mục của bạn
4customers <- read.csv("Mall_Customers.csv") 
5
6customers <- rename(
7  customers, 
8  SpendingScore = `Spending.Score..1.100.`,
9  AnnualIncome = `Annual.Income..k..`
10)

Dữ liệu sau đây chứa thông tin cơ bản về khách hàng như “Mã khách hàng, độ tuổi, giới tính, thu nhập hàng năm và điểm chi tiêu”. Điểm chi tiêu được gán cho mỗi khách hàng dựa trên các tham số xác định như hành vi khách hàng và dữ liệu mua sắm như sau:

1head(customers)
2
3##   CustomerID Gender Age AnnualIncome SpendingScore
4## 1          1   Male  19           15            39
5## 2          2   Male  21           15            81
6## 3          3 Female  20           16             6
7## 4          4 Female  23           16            77
8## 5          5 Female  31           17            40
9## 6          6 Female  22           17            76

Sau đó, để kiểm tra cấu trúc dữ liệu ta sử dụng hàm str, còn hàm sum(is.na()) được sử dụng để đảm bảo rằng không có ô dữ liệu nào bị trống:

1str(customers)
2## 'data.frame':    200 obs. of  5 variables:
3##  $ CustomerID   : int  1 2 3 4 5 6 7 8 9 10 ...
4##  $ Gender       : chr  "Male" "Male" "Female" "Female" ...
5##  $ Age          : int  19 21 20 23 31 22 35 23 64 30 ...
6##  $ AnnualIncome : int  15 15 16 16 17 17 18 18 19 19 ...
7##  $ SpendingScore: int  39 81 6 77 40 76 6 94 3 72 ...

1sum(is.na(customers))
2## [1] 0

4. Thực hiện phân cụm

Để phân cụm nhóm khách hàng sẵn sàng chi tiêu cùng với các yếu tố nhân khẩu học của họ, ta sẽ thực hiện thuật toán phân cụm như sau.

Để tìm giá trị K tối ưu, chúng ta sẽ vẽ biểu đồ Total Within Sum of Squares (WSS). Total Within Sum of Squares (WSS) là một khái niệm quan trọng trong thuật toán phân cụm K-means, và nó dùng để đo độ phân tán của dữ liệu trong một cụm sau khi dữ liệu đã được phân nhóm. Để biết giá trị K tối ưu thông qua Total Within Sum of Squares (WSS), một phương pháp thường được sử dụng gọi là Elbow Method (Phương pháp “khủyu tay”).

Vẽ một biểu đồ với trục X là số lượng cụm K, và trục Y là giá trị WSS tương ứng. Bạn sẽ thấy rằng WSS giảm dần khi K tăng. Vì khi có nhiều cụm hơn, các điểm dữ liệu trong cụm sẽ gần với trung điểm của chúng hơn, dẫn đến tổng khoảng cách ngắn hơn. Khi K còn nhỏ, WSS sẽ giảm nhanh. Tuy nhiên, sau một mức K nào đó, tốc độ giảm của WSS sẽ chậm lại. Trong đó có một điểm gọi là điểm khuỷu tay, điểm mà WSS bắt đầu chậm lại đáng kể, nhưng sau điểm này, K tăng không ảnh hưởng đáng kể tới WSS nữa.

Tại điểm khuỷu tay, lúc này, K là số lượng cụm lý tưởng, vì nó đạt được sự cân bằng giữa phân cụm tốt và việc giữ cho cụm không quá phân tán.

Ngoài ra, hai cách khác giúp độc giả có thể tìm giá trị K tối ưu bao gồm: “Trung bình Silhoutte, và Gap-statistic”.

4.1. Phân cụm theo tuổi và điểm chi tiêu

Total WSS được vẽ như sau:

1kdf1 <- customers[,c(3,5)]
2set.seed(123)
3fviz_nbclust(kdf1, kmeans, method = "wss")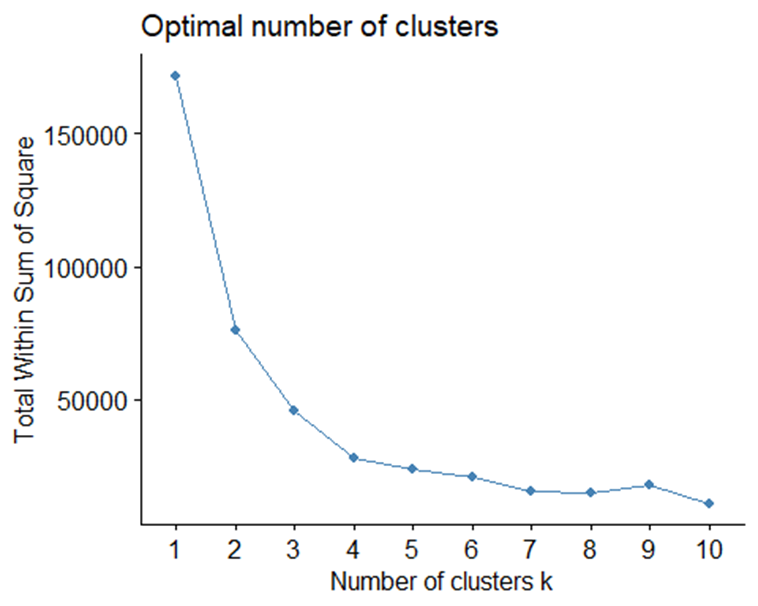

Từ biểu đồ trên, chúng ta thấy rằng từ giá trị k = 4 trở đi, độ biến động của Total WSS không thay đổi đáng kể nữa. Qua đó, ta có thể xác định được rằng điểm khuỷu tay nằm ở vị trí k = 4, đồng nghĩa với việc rằng số cụm chúng ta sẽ chọn là 4.

Để tính ra giá trị K-means, và phân cụm nhóm khách hàng, ta sử dụng hàm sau:

1cl1 <- kmeans(kdf1, 4, nstart = 10)

Sau đó, chúng ta tiến hành vẽ biểu đồ phân cụm như sau:

1ggplot(
2  kdf1, 
3  aes(x = Age, y = SpendingScore)
4) + 
5  geom_point(
6    stat = "identity",
7     aes(color = as.factor(cl1$cluster))
8  ) +
9  scale_color_discrete(
10    name=" ",
11    labels=c(
12      "Tệp khách hàng mục tiêu",
13      "Tệp khách hàng trẻ có tiềm năng",
14      "Tệp khách hàng ít tiềm năng",
15      "Tệp khách hàng cao tuổi tiềm năng"
16    )
17  ) +
18  ggtitle(
19    "Mall Customer Segments",
20    subtitle = "K-means Clustering"
21  ) + 
22  ylab("Điểm chi tiêu")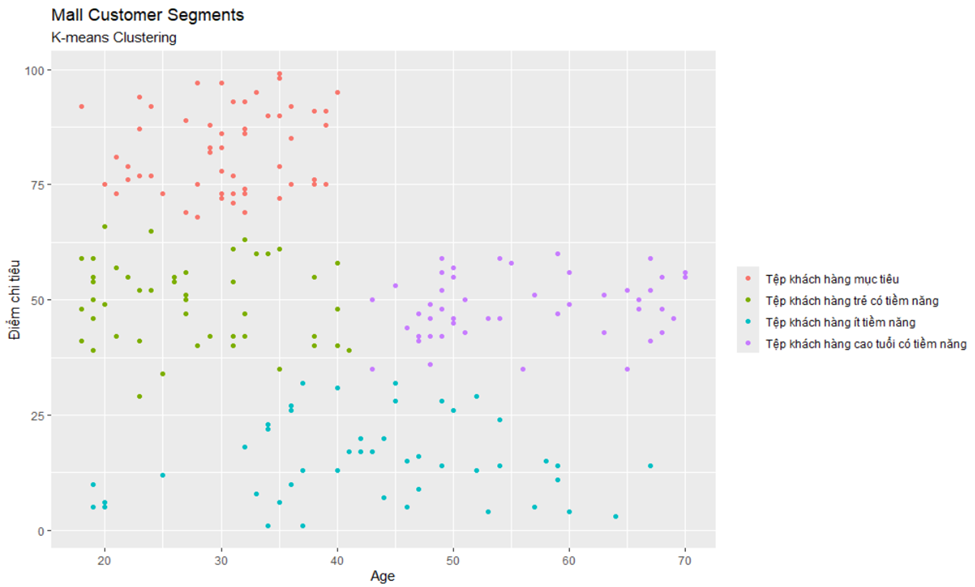

Giải thích:

• Tệp khách hàng mục tiêu cho thấy rằng nhóm này tập trung một lượng lớn khách hàng dưới 40 tuổi với chi tiêu ở mức cao. Cho thấy rằng tệp khách hàng này mang nhiều tiềm năng nhất trong bốn cụm khách hàng, và nên là khách hàng mục tiêu của trung tâm này.
• Tệp khách hàng trẻ có tiềm năng cho thấy rằng nhóm này tập trung một lượng lớn khách hàng dưới 40 tuổi chỉ chi tiêu ở mức trung bình. Cho thấy rằng tệp khách hàng này có tiềm năng để trung tâm hướng tới.
• Tệp khách hàng ít tiềm năng cho thấy rằng nhóm này tập trung một lượng lớn khách hàng trải đều trên mọi độ tuổi với chi tiêu ở mức thấp. Cho thấy rằng đây là một tệp khách hàng không quá tiềm năng.
• Tệp khách hàng cao tuổi cho thấy rằng nhóm này tập trung một lượng lớn khách hàng trên 40 tuổi chỉ chi tiêu ở mức trung bình. Cho thấy rằng tệp khách hàng này có tiềm năng để trung tâm hướng tới.

4.2. Phân cụm theo thu nhập hàng năm và điểm chi tiêu

Sau khi phân loại khách hàng dựa trên độ tuổi và mức độ chi tiêu của họ, chúng ta sẽ tiếp tục phân tích với một yếu tố nhân khẩu học khác đó là thu nhập hàng năm của khách hàng. Qua cách phân cụm này, chúng ta sẽ tìm ra được kế hoạch để phân bổ giá trị hàng hóa nhằm phù hợp với các cụm khách hàng.

Total WSS được vẽ như sau:

1kdf2 <- customers[,4:5]
2set.seed(123)
3fviz_nbclust(kdf2, kmeans, method = "wss")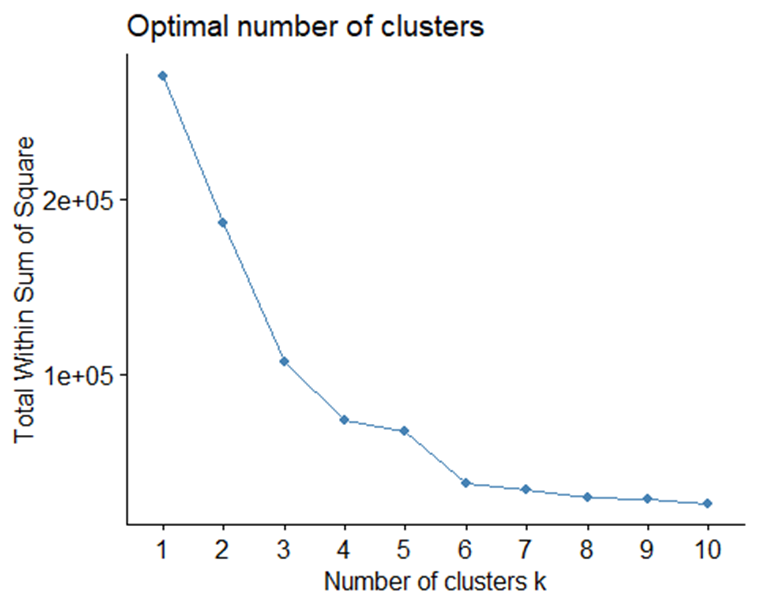

Từ biểu đồ trên, chúng ta thấy rằng từ giá trị k = 6 trở đi, độ biến động của Total WSS giảm mạnh. Tuy nhiên, sau khi trực quan hóa dữ liệu, ta sẽ thấy rằng số lượng cụm tối ưu nên là k = 5. Để giải thích chi tiết hơn về trường hợp này, mục 5 sẽ giới thiệu về biểu đồ kiểm tra chất lượng số cụm, và giải thích chi tiết về trường hợp này.

Để tính ra giá trị K-means, và phân cụm nhóm khách hàng, ta sử dụng hàm sau:

1cl2 <- kmeans(kdf2,5, nstart = 10)

Sau đó, chúng ta tiến hành vẽ biểu đồ phân cụm:

1ggplot(
2  kdf2,
3    aes(x = AnnualIncome, y = SpendingScore)
4) + 
5  geom_point(
6    stat = "identity", 
7    aes(color = as.factor(cl2$cluster))
8  ) +
9  scale_color_discrete(
10    name=" ",
11    labels=c(
12      "Tệp khách hàng ít tiềm năng 1",
13      "Tệp khách hàng ít tiềm năng 2",
14      "Tệp khách hàng có tiềm năng",
15      "Tệp khách hàng tiềm năng 1",
16      "Tệp khách hàng tiềm năng 2"
17    )
18  ) +
19  ggtitle(
20    "Mall Customer Segments", 
21    subtitle = "K-means Clustering"
22  ) + 
23  ylab("Điểm chi tiêu") + 
24  xlab("Thu nhập hàng năm (k$)")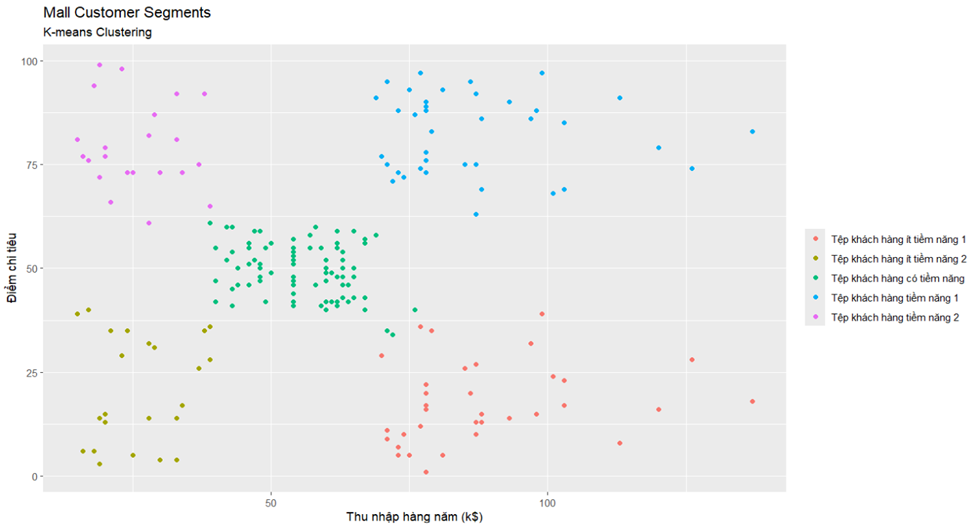 

Giải thích:

• Tệp khách hàng ít tiềm năng 1 gồm những khách hàng có mức thu nhập trên $50000 nhưng có xu hướng chi tiêu ở mức thấp. Cho thấy rằng đây không phải là một tệp khách hàng tiềm năng.
• Tệp khách hàng ít tiềm năng 2 gồm những khách hàng có mức thu nhập dưới $50000 và có xu hướng chi tiêu thấp. Cho thấy rằng đây không phải là một tệp khách hàng tiềm năng.
• Tệp khách hàng có tiềm năng là nhóm khách hàng có mức thu nhập trong khoảng $35000 - $75000 và có điểm chi tiêu ở mức trung bình. Cho thấy rằng đây là một tệp khách hàng có tiềm năng, nhưng chưa phải là khách hàng mục tiêu.
• Tệp khách hàng tiềm năng 1 gồm những khách hàng có mức thu nhập trên $50000 với mức chi tiêu cao. Đây là nhóm khách hàng với nhiều tiềm năng nhất, đồng thời là nhóm khách hàng mục tiêu mà trung tâm nên hướng tới.
• Tệp khách hàng tiềm năng 2 bao gồm các khách hàng có mức thu nhập dưới $50000 với mức chi tiêu cao. Cho thấy rằng đây là một tệp khách hàng tiềm năng và nằm trong nhóm khách hàng mục tiêu.

5. Kiểm tra chất lượng phân cụm

Qua bài thực hành phía trên, nếu độc giả cảm thấy chưa thuyết phục với số phân cụm k tính ra được từ Total WSS, thì sau đây là phương thức mà độc giả có thể sử dụng để kiểm tra chất lượng của số cụm đã được tính ra phía trên.

Giải thích kiểm tra chất lượng phân cụm bằng biểu đồ silhouette:

Chỉ số Silhouette là một phương pháp để đánh giá chất lượng phân cụm, đặc biệt hữu ích trong các bài toán phân cụm như K-Means hoặc phân cụm phân cấp. Chỉ số này cho phép ta đo lường mức độ phù hợp của các điểm dữ liệu trong cùng cụm với nhau và so sánh với các cụm khác. Cụ thể, chỉ số Silhouette sẽ cung cấp giá trị từ -1 đến 1 cho từng điểm dữ liệu, biểu diễn mức độ phù hợp của điểm đó với cụm mà nó đang thuộc về so với các cụm khác.

Các cụm có chất lượng cao cần đáp ứng hai yếu tố, một là đa phần các số quan sát phải lớn hơn 0, hai là phải có nhiều quan sát trên trung bình Silhouette khi so sánh trên biểu đồ.

5.1. Chất lượng phân cụm điểm chi tiêu và độ tuổi khách hàng

1test1 <- silhouette(cl1$cluster, dist(kdf1))
2fviz_silhouette(test1)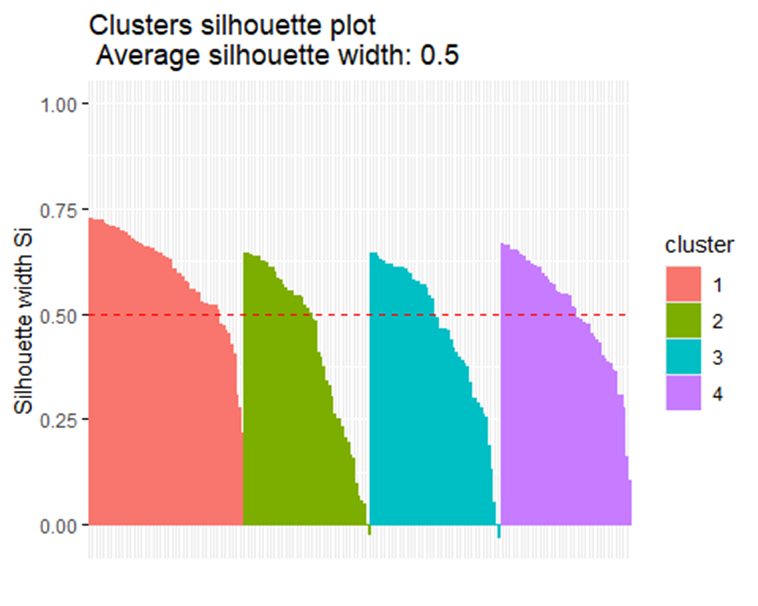

Từ biểu đồ trên, ta thấy rằng tại số phân cụm k = 4 có đa phần số quan sát lớn hơn 0, và có nhiều biến quan sát trên đường trung bình. Cho thấy rằng số cụm bằng 4 đảm bảo chất lượng để phân cụm

5.2. Chất lượng phân cụm điểm chi tiêu và thu nhập hàng năm của khách hàng

1test2 <- silhouette(cl2$cluster, dist(kdf2))
2fviz_silhouette(test2)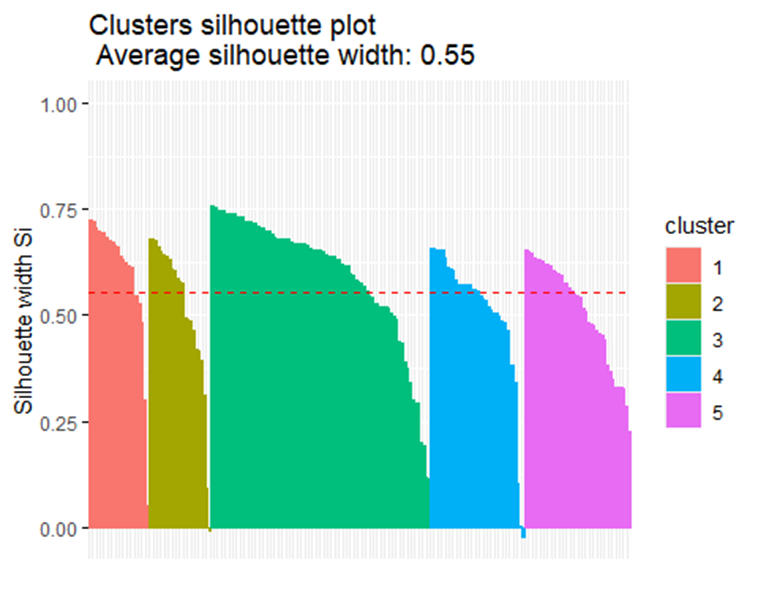

Từ biểu đồ trên, với số cụm là 5 đều cho thấy rằng các cụm đều đạt chất lượng, đa phần quan sát lớn hơn 0 và lớn hơn giá trị trung bình silhouette. Bây giờ, chúng ta sẽ kiểm tra xem rằng khi tăng số cụm lên 6 thì có đạt được chất lượng như mong muốn không.

1cl2 <- kmeans(kdf2,6, nstart = 10)
2test2 <- silhouette(cl2$cluster, dist(kdf2))

Biểu đồ được trực quan hóa như sau:

1fviz_silhouette(test2)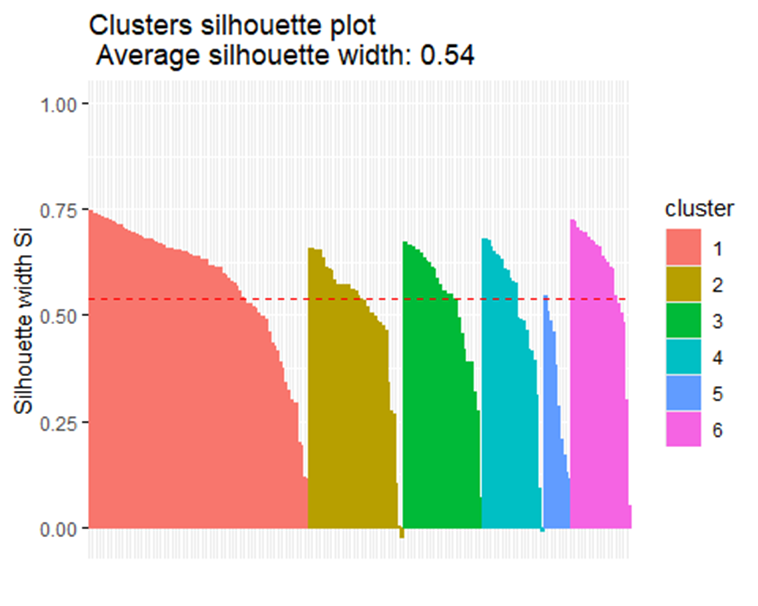

Mặc dù, khi kiểm tra điểm khuỷu tay cho thấy kết quả số cụm tối ưu là 6, nhưng khi kiểm tra chất lượng của các cụm thì cụm số 6 lại không đạt được chất lượng cao như mong muốn. Đó là bởi cụm số 6 bao gồm những biến ngoại lai, tạo nên cụm riêng biệt này. Tuy nhiên, việc tăng số cụm để phù hợp với các điểm ngoại lai có thể làm giảm tính nhất quán và sự gắn kết tự nhiên của các cụm ban đầu.

Do đó, dù số cụm tối ưu được tính ra là k=6, nhưng số cụm hợp lý và chất lượng hơn để phản ánh cấu trúc dữ liệu một cách toàn vẹn trong biểu đồ này là k=5

6. Nhược điểm

Bên cạnh sự hiệu quả của thuật toán trong việc phân loại dữ liệu đó, phân cụm k-means vẫn có một vài nhược điểm nhất định.

• Khi xảy ra trường hợp tồn tại các dữ liệu ngoại lai (outliers) như bên trên các dữ liệu đó có thể làm sai lệch trọng tâm của cụm, dẫn đến kết quả phân cụm khác với số lượng phân cụm thực sự cần thiết.
• K-means chỉ hỗ trợ dữ liệu định lượng (biến liên tục), không chạy được cho dữ liệu định tính (biến phân loại, ví dụ: giới tính, đặc điểm nhân khẩu học, ...). Do đó bạn có thể tìm hiểu thêm phương pháp K-mode hoặc K-prototype để hỗ trợ loại dữ liệu định tính này.
• Ngoài ra, thuận toán K-means không phù hợp với trường hợp các cụm có kích thước, mật độ, hình dạng, và độ quan trọng khác nhau. Bởi K-means giả định rằng các cụm có dạng hình cầu và có kích thước tương tự nhau, điều này không phải lúc nào cũng đúng.
• Ngoài ra, nếu số cụm tối ưu không rõ ràng, K-means có thể cho kết quả không tối ưu, trường hợp đó những phương pháp như phân cụm trên mật độ (DBSCAN) sẽ phù hợp hơn.

7. Tổng kết

Thuật toán phân cụm k-means là một thuật toán phù hợp với tệp dữ liệu cần được phân loại hoặc nhận diện kiểu mẫu. Ngoài ra, thuật toán này giúp cho người dùng dễ dàng phân loại các nhóm dữ liệu mới từ bộ dữ liệu phức tạp. Thuật toán này phù hợp với những trường hợp dữ liệu tuyến tính, khoảng cách giữa các biến có thể tính được, hoặc dữ liệu có cấu trúc. Trong những trường hợp này, K-means được lựa chọn bởi độ đơn giản, dễ hiểu, thực hiện, và tốc độ của thuật toán.