[BLOG 006] Phân tích chuỗi thời gian với ngôn ngữ R (Phần 1)

Time series Analysis (phân tích dữ liệu chuỗi thời gian) là một trong những chủ đề rộng lớn và phức tạp, ở bài viết này chúng ta sẽ thực hiện một số xử lý về dữ liệu và phân tích time series trong R.

Đây là chuỗi bài viết từ cơ bản đến nâng cao về xử lý dữ liệu time series với ngôn ngữ R.

1. Đọc dữ liệu chuỗi thời gian (time series)

Dữ liệu thực hành được sử dụng tại bài viết này là AirPassengers, đây là bộ dữ liệu có sẵn trong R về thông tin số lượng khách du lịch hàng không theo tháng.

1data("AirPassengers")
2AP <- AirPassengers
3str(AP)
4# Time-Series [1:144] from 1949 to 1961: 112 118 132 129 121 135 148 148 136 119 ...

Đây là dữ liệu theo tháng từ năm 1949 đến năm 1961 với 144 tháng (144 quan sát)

Sử dụng hàm ts để chuyển sang dạng timeseries data, ta nhập frequency là chu kỳ lặp lại trong một năm, ở đây vì đây là dữ liệu theo tháng nên frequency = 12, giả sử nếu dữ liệu theo ngày thì frequency = 365

1ts(AP, frequency = 12, start=c(1949,1))
2
3# Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
4# 1949 112 118 132 129 121 135 148 148 136 119 104 118
5# 1950 115 126 141 135 125 149 170 170 158 133 114 140
6# 1951 145 150 178 163 172 178 199 199 184 162 146 166
7# 1952 171 180 193 181 183 218 230 242 209 191 172 194
8# 1953 196 196 236 235 229 243 264 272 237 211 180 201
9# 1954 204 188 235 227 234 264 302 293 259 229 203 229
10# 1955 242 233 267 269 270 315 364 347 312 274 237 278
11# 1956 284 277 317 313 318 374 413 405 355 306 271 306
12# 1957 315 301 356 348 355 422 465 467 404 347 305 336
13# 1958 340 318 362 348 363 435 491 505 404 359 310 337
14# 1959 360 342 406 396 420 472 548 559 463 407 362 405
15# 1960 417 391 419 461 472 535 622 606 508 461 390 432

Sử dụng hàm plot để vẽ biểu đồ

1plot(AP)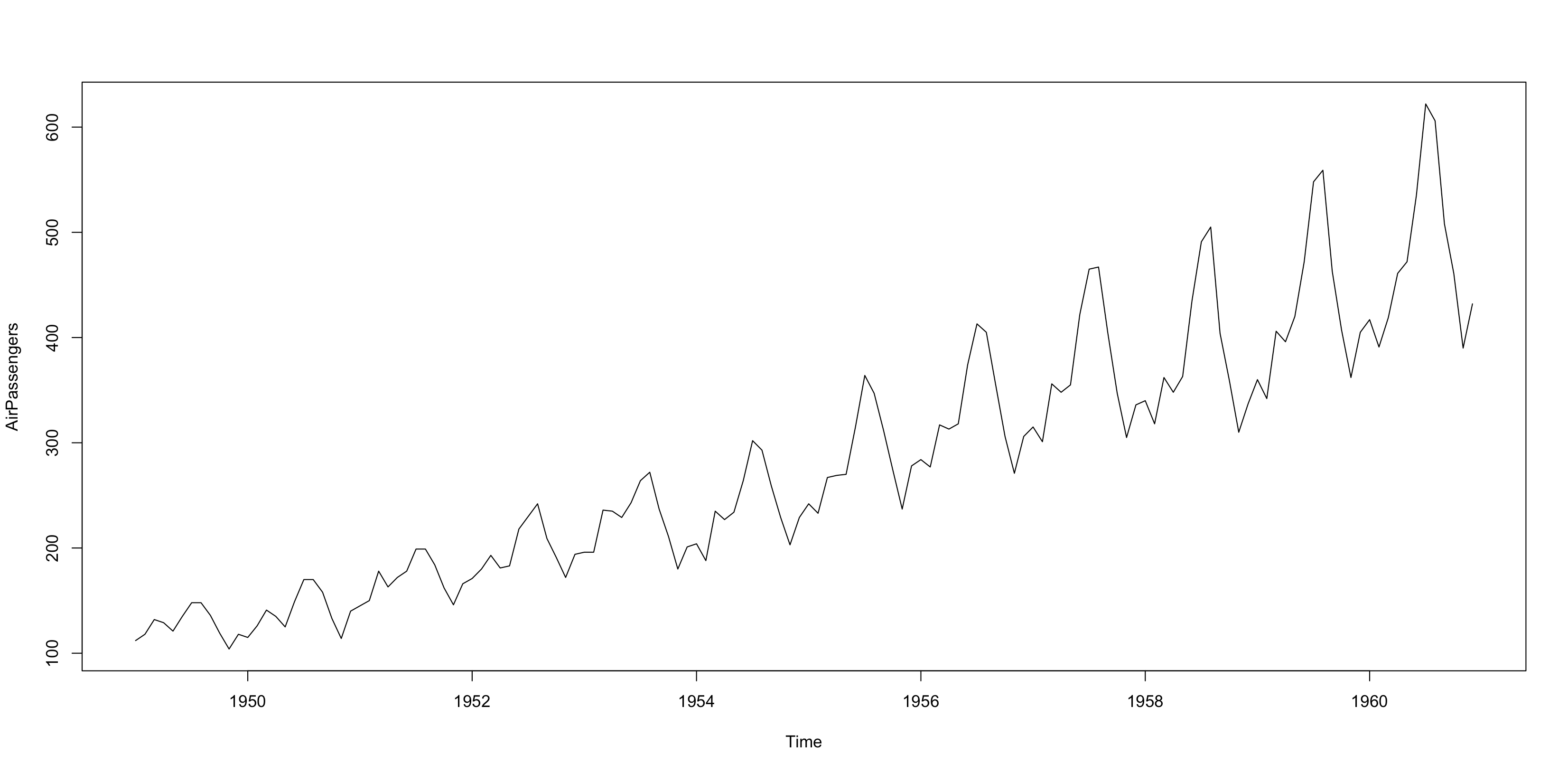

Với dữ liệu này ta thấy có sự ổn định (stationary) và tăng dần theo thời gian

2. Phân tích chuỗi thời gian

2.1. Log transform

Log transform và một kỹ thuật giúp chuyển đổi dữ liệu giúp dữ liệu giúp tăng tính ổn định nhưng vẫn đảm bảo được những đặc trưng của dữ liệu.

Thường được sử dụng cho những chuỗi thời gian có sự biến động bất thường (nonstationary data). Ví dụ ta sử dụng cho dữ liệu chuỗi thời gian cho dữ liệu trên:

1AP <- log(AP)
2plot(AP)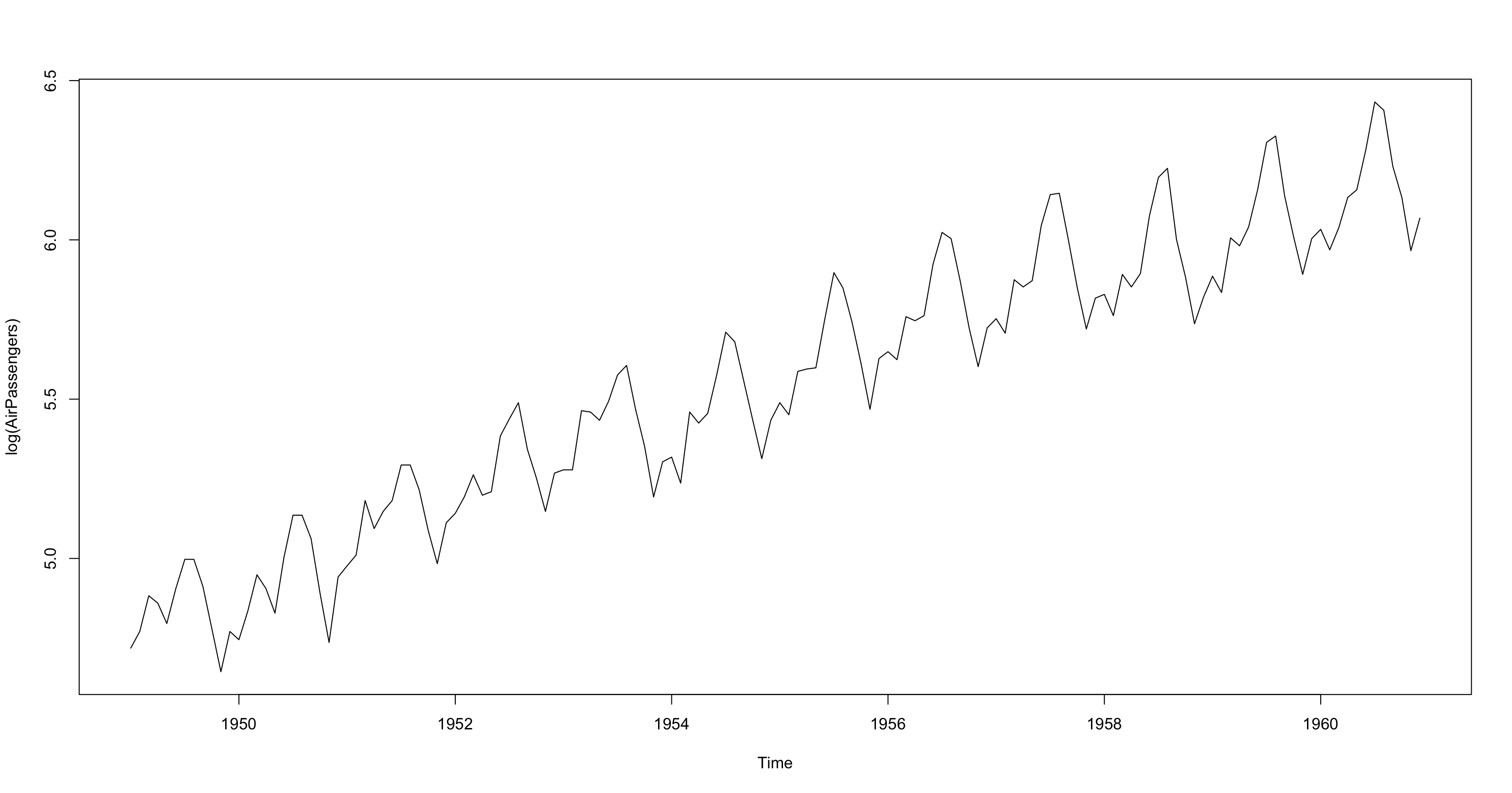

Ta thấy sau khi chuyển đổi, dữ liệu dạng logarith hoá đã có tính ổn định hơn so với dữ liệu ban đầu, ta có thể thấy rõ được sự biến động và tăng trưởng đều theo thời gian từ đầu kì đến cuối kì.

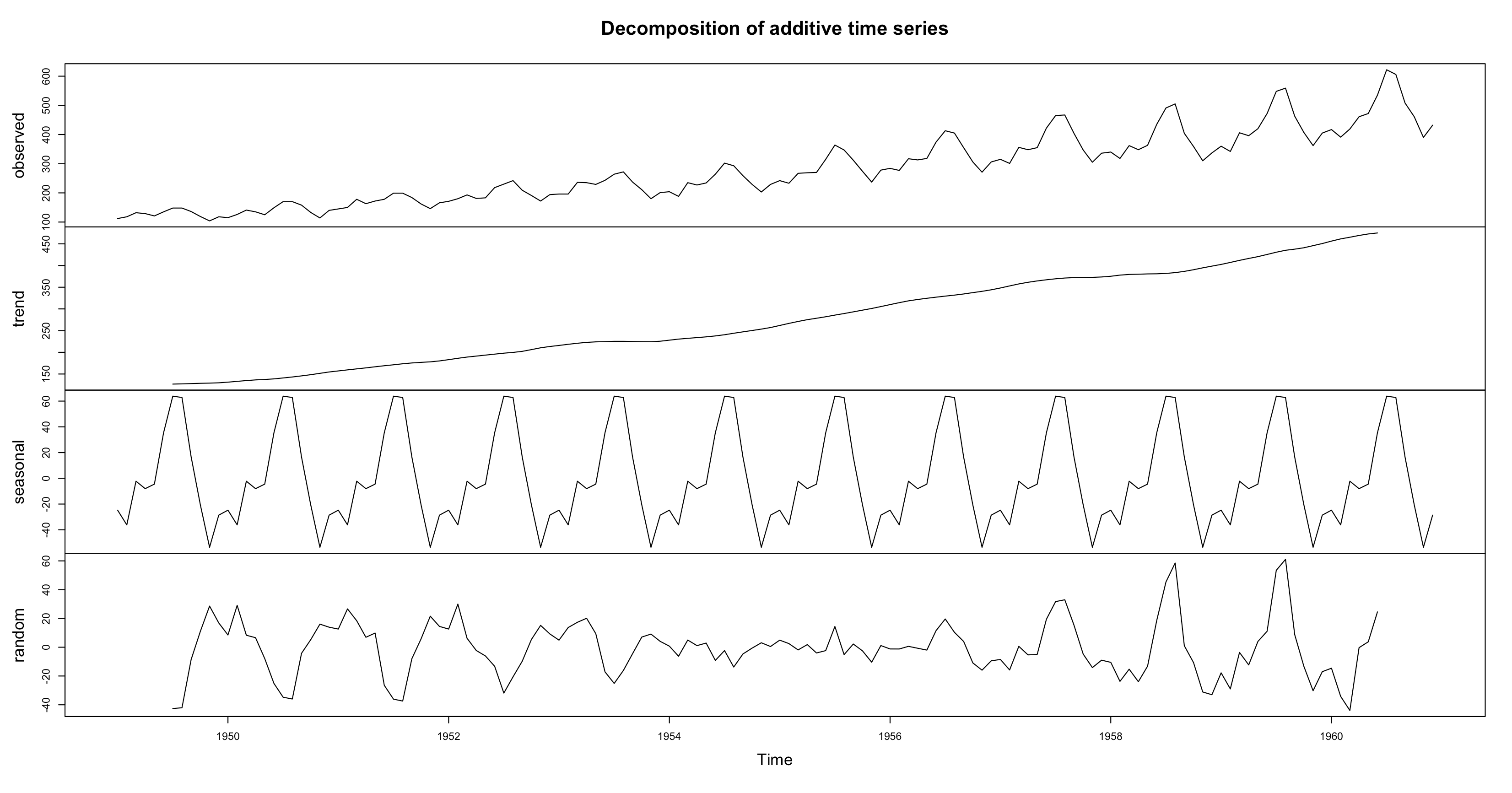
2.2. Phân rã chuỗi thời gian (Decomposition of time series)

Như bạn có thể đã biết, chuỗi thời gian được tạo bởi 4 thành phần:

• Xu thế (Secular Trend): biểu thị cho sự tăng giảm đều theo thời gian.
• Thời vụ (Seasonal Variation): là những thay đổi tăng giảm lặp đi lặp lại trong một năm (ta có thể nhìn rõ về hiện tượng thời vụ đối với dữ liệu khách du lịch hàng không AirPassengers, ta thấy trong một năm có những tháng cao điểm của du lịch ví dụ từ tháng 5 đến tháng 8, khách đi du lịch rất nhiều và có những tháng thấp điểm, khách hầu như không có nhu cầu đi du lịch, ta sẽ xem xét rõ hơn về hiện tượng thời vụ đối với dữ liệu này tại phần dưới.
• Chu kì (Cyclical Variation): là những biến động lặp đi lặp lại trong nhiều năm. Lưu ý khác với thời vụ và những biến động trong 1 năm, chu kì là những biến động cho nhiều năm. Thông thường dữ liệu ta không đủ để phân tích yếu tố này, vì để xác định yếu tố chu kì, ta phải có lượng dữ liệu đủ lớn qua các năm và số lượng năm đủ dài, ít nhất là 20 năm trở lên mới có thể phần nào xác định được yếu tố này.
• Nhiễu (Irregular Variation): là những thay đổi ngẫu nhiên, bất thường, không có quy luật, không xác định được qua thời gian.

Ta gọi: $Y$ cho chuỗi thời gian gốc, $T$ là phần xu thế, $S$ là thành phần thời vụ, $C$ là thành phần chu kì và cuối cùng $I$ là thành phần nhiễu.

Ta có hai cách để phân rã chuỗi thời gian, đầu tiên là phân rã dạng cộng:

Thứ hai là phân rã dạng nhân:

Ta sẽ sử dụng phân rã dạng cộng cho dữ liệu trên như sau:

1decomp <- decompose(AP)
2decomp$figure
3# [1] -0.085815019 -0.114412848  0.018113355 -0.013045611 -0.008966106  0.115392997  0.210816435  0.204512399  0.064836351 -0.075271265 -0.215845612 -0.100315075
4
5plot(decomp$figure,
6     type = 'b',
7     xlab = 'Month',
8     ylab = 'Seasonality Index',
9     col = 'blue',
10     las = 2)

Ta sử dụng hàm plot để trực quan kết quả:

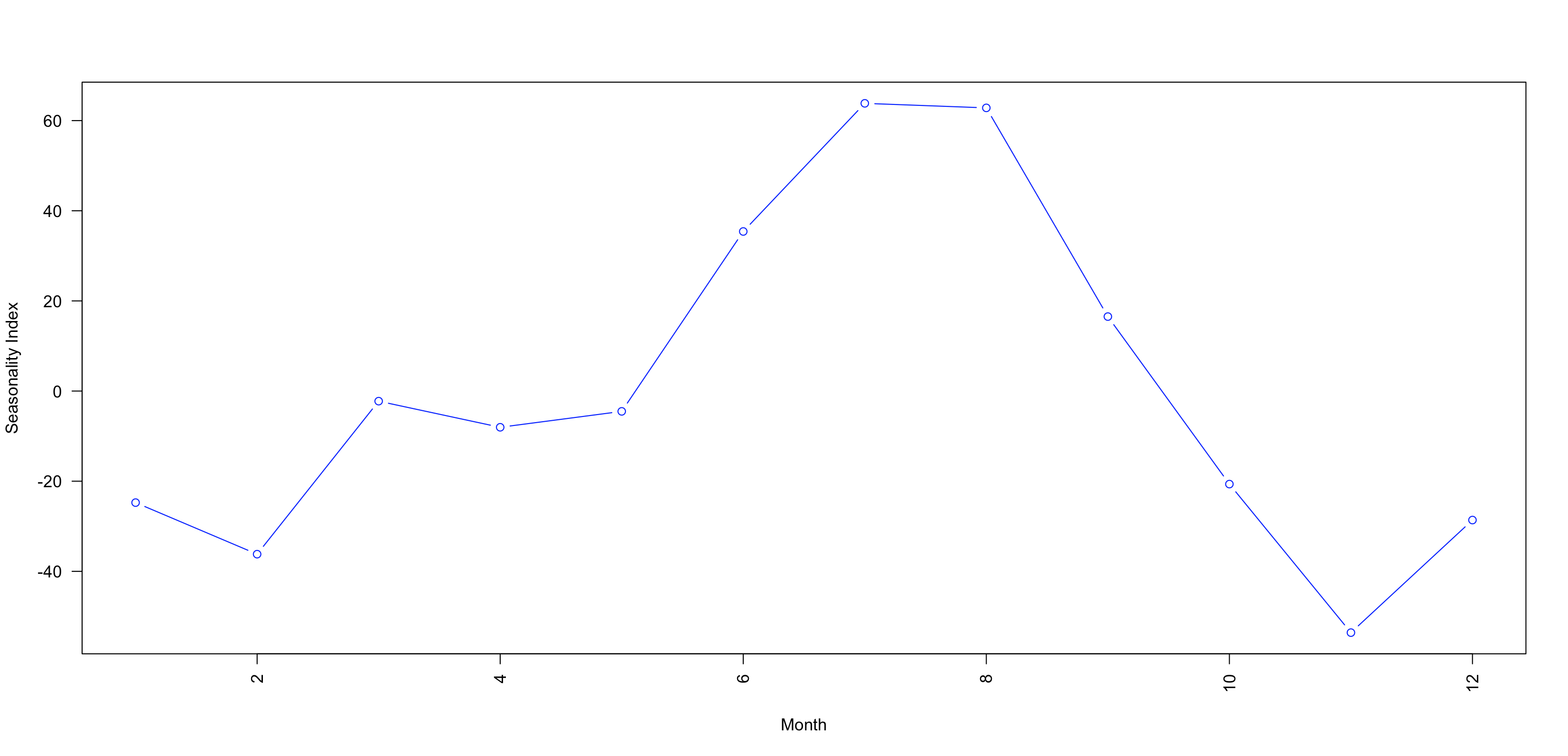
Lưu ý giữ liệu được phân rã đang ở dạng log, ta thấy được phần trăm thay đổi về xu thế qua các tháng về số lượng khách du lịch như sau:

Từ tháng 11 trở đi ta thấy được lượng khách sẽ giảm đi ít nhất 20% so với bình quân, và từ tháng 7 đến tháng 8, lượng khách du lịch sẽ tăng ít nhất 20% - 60% so với bình quân.

Tiếp tục, sử dụng hàm plot để xem kết quả về các thành phần được phân rã

1plot(decomp)

Ta thấy hàm trên chỉ phân rã 3 thành phần cơ bản là xu thế, thời vụ và nhiễu. Không có thành phần chu kì vì không đủ dữ liệu để thực hiện.

3. Forecasting

3.1. ARIMA – Autoregressive Integrated Moving Average

Ta sử dụng phương pháp ARIMA để thực hiện dự báo, đây là một trong những phương pháp phổ biến và dễ thực hiện.

Với ARIMA ta sẽ sử dụng thông số mặc định ARIMA(0,1,1). Tức AR=0, I = 1, MA = 1. Với thông số này ta chỉ lấy sai phân 1 kì, và có chỉ sử dụng thành phần trung bình trượt MA mà không sử dụng tự hồi quy (AR).

1library(forecast)
2model <- auto.arima(AP)
3model
4# Series: AP
5# ARIMA(0,1,1)(0,1,1)[12]
6# Coefficients:
7#           ma1     sma1
8#       -0.4018  -0.5569
9# s.e.   0.0896   0.0731
10# sigma^2 estimated as 0.001371:  log likelihood=244.7
11# AIC=-483.4   AICc=-483.21   BIC=-474.77

AIC và BIC là chỉ số được tính trên sai số và độ phức tạp của mô hình, các chỉ số này càng cao thì mô hình có nhiều sai số hoặc độ phức tạp lớn.

AIC và BIC giúp ta so sánh để chọn được mô hình tốt nhất.

3.2. Đồ thị ACF và PACF

Luôn phải xem xét đến đồ thị ACF và PACF khi xử lý dữ liệu chuỗi thời gian để xác định thành phần tự tương quan, tức trả lời cho câu hỏi dữ liệu ở quá khứ có ảnh hưởng tới dữ liệu ở hiện tại hay không?

Và đối với mô hình ARIMA đã chạy, để mô hình hoạt động tốt, phần sai số hay phần dư của mô hình (residuals) phải hoàn toàn là nhiễu, tức trong đó không được có hiện tượng phần dư tự tương quan.

1acf(model$residuals, main = 'Correlogram')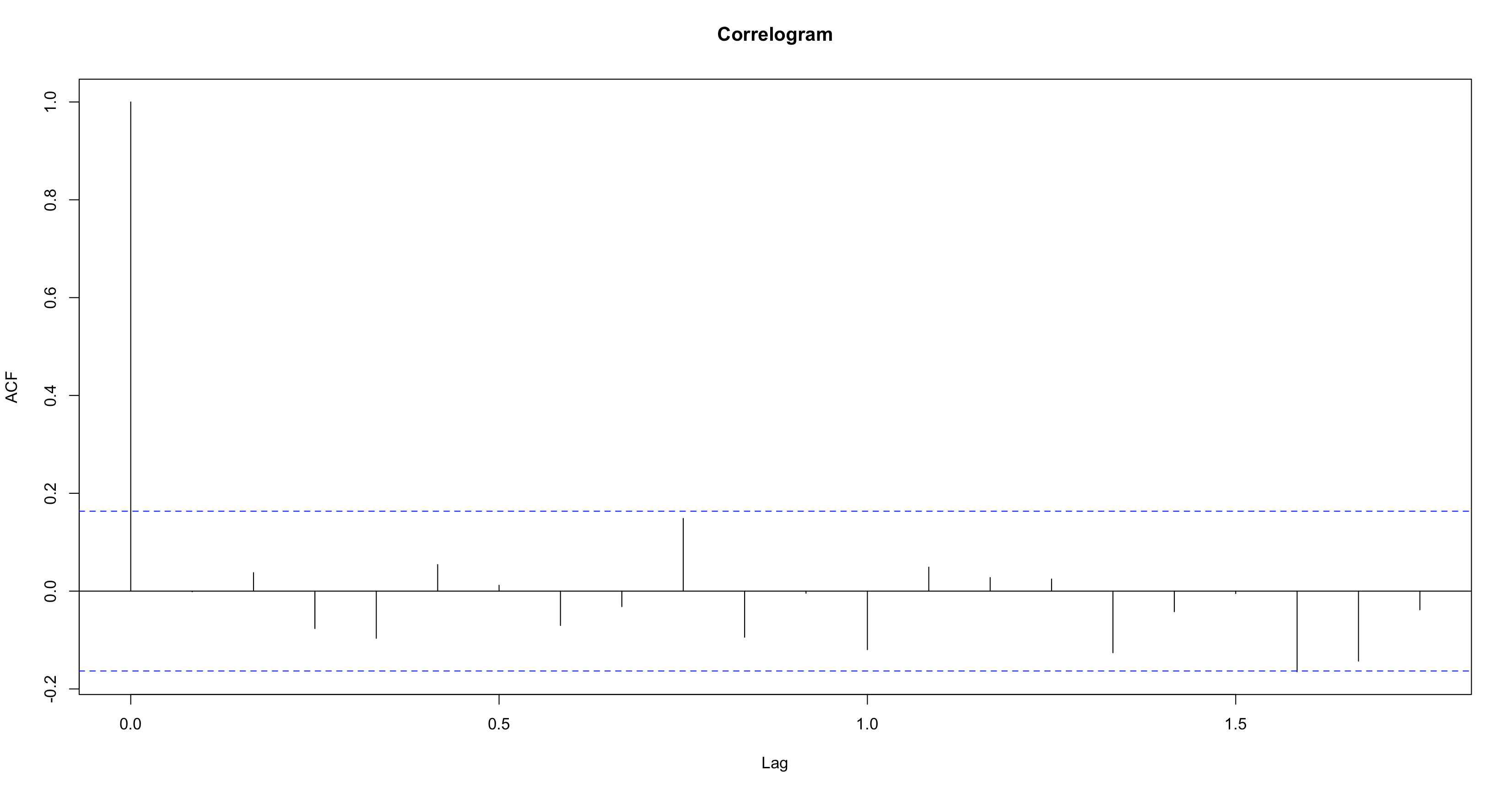

Đường nét đứt là ngưỡng có ý nghĩa thống kê. Chỉ ACF tại lag 0 đã vượt qua vượt qua ngưỡng này. Và tại lag 1 và 1.5 thì chỉ chạm đến ngưỡng này.

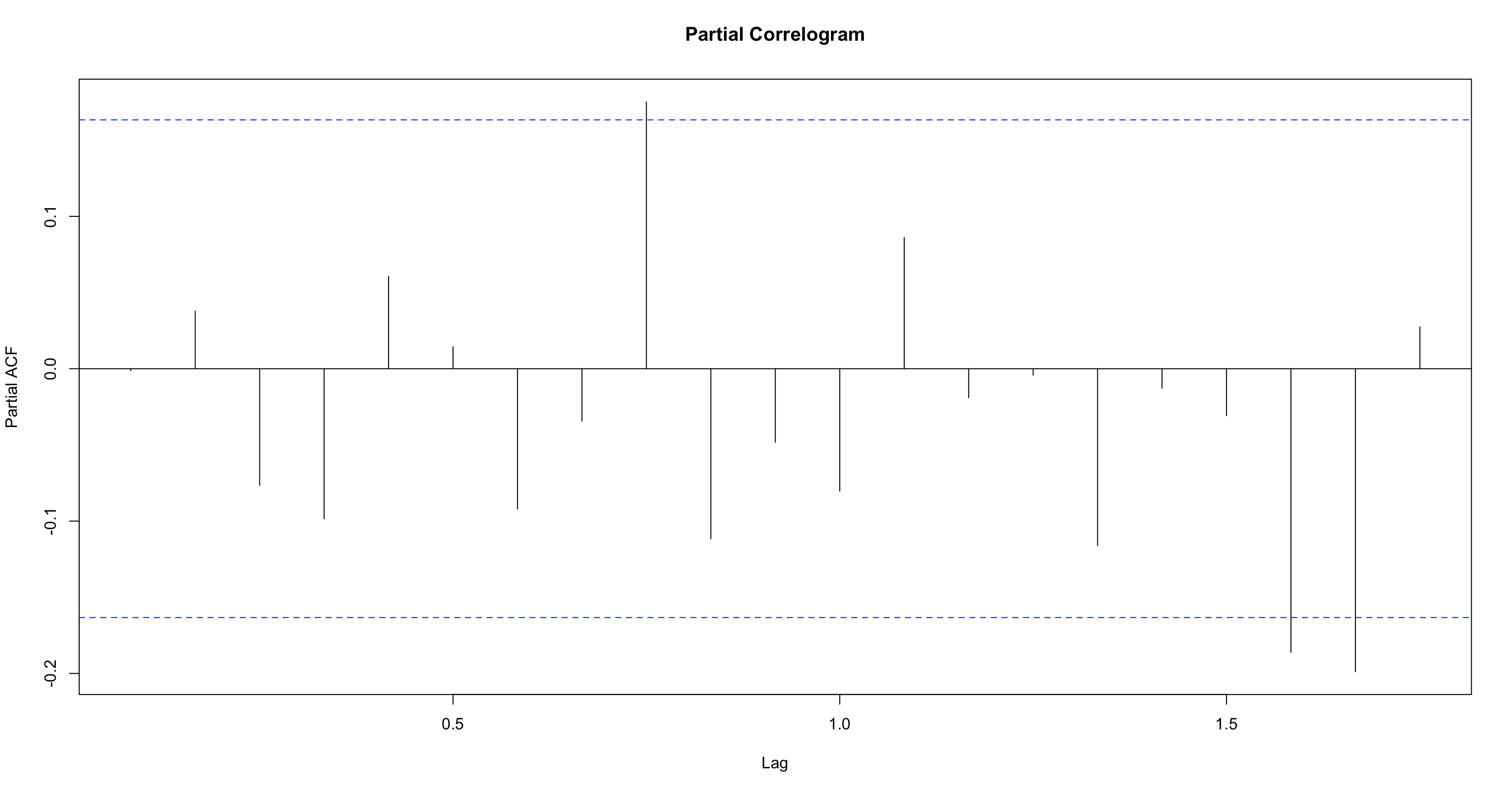
Và với PACF thì hầu hết các lag đều nằm trong 2 ngưỡng này.

3.3. Ljung-Box test

Kiểm định Ljung–Box (được đặt tên theo Greta M. Ljung và George E. P. Box) là một loại kiểm định thống kê xem liệu bất kỳ nhóm tự tương quan nào của chuỗi thời gian có khác 0 hay không. Thay vì kiểm tra tính ngẫu nhiên ở mỗi độ trễ riêng biệt, nó kiểm tra tính ngẫu nhiên "tổng thể" dựa trên một số độ trễ và do đó là một phép thử portmanteau.

Ta thực hiện kiểm định với phần dư từ mô hình ARIMA bên trên:

1Box.test(model$residuals, lag=20, type = 'Ljung-Box')
2# Box-Ljung test
3# data:  model$residuals
4# X-squared = 17.688, df = 20, p-value = 0.6079

Với p-value = 0.6079, không có sự khác biệt đáng kể nào được quan sát cho thấy hiện tượng tự tương quan được quan sát ở độ trễ 1 và 1,5 có thể là do random chance. Với kiểm định này, chưa có bằng chứng để khẳng định phần dư của mô hình gặp hiện tượng tự tương quan.

3.4. Phân phối của phần dư (Residuals Distribution)

1hist(model$residuals,
2     col = 'red',
3     xlab = 'Error',
4     main = 'Histogram of Residuals',
5     freq = FALSE)
6lines(density(model$residuals))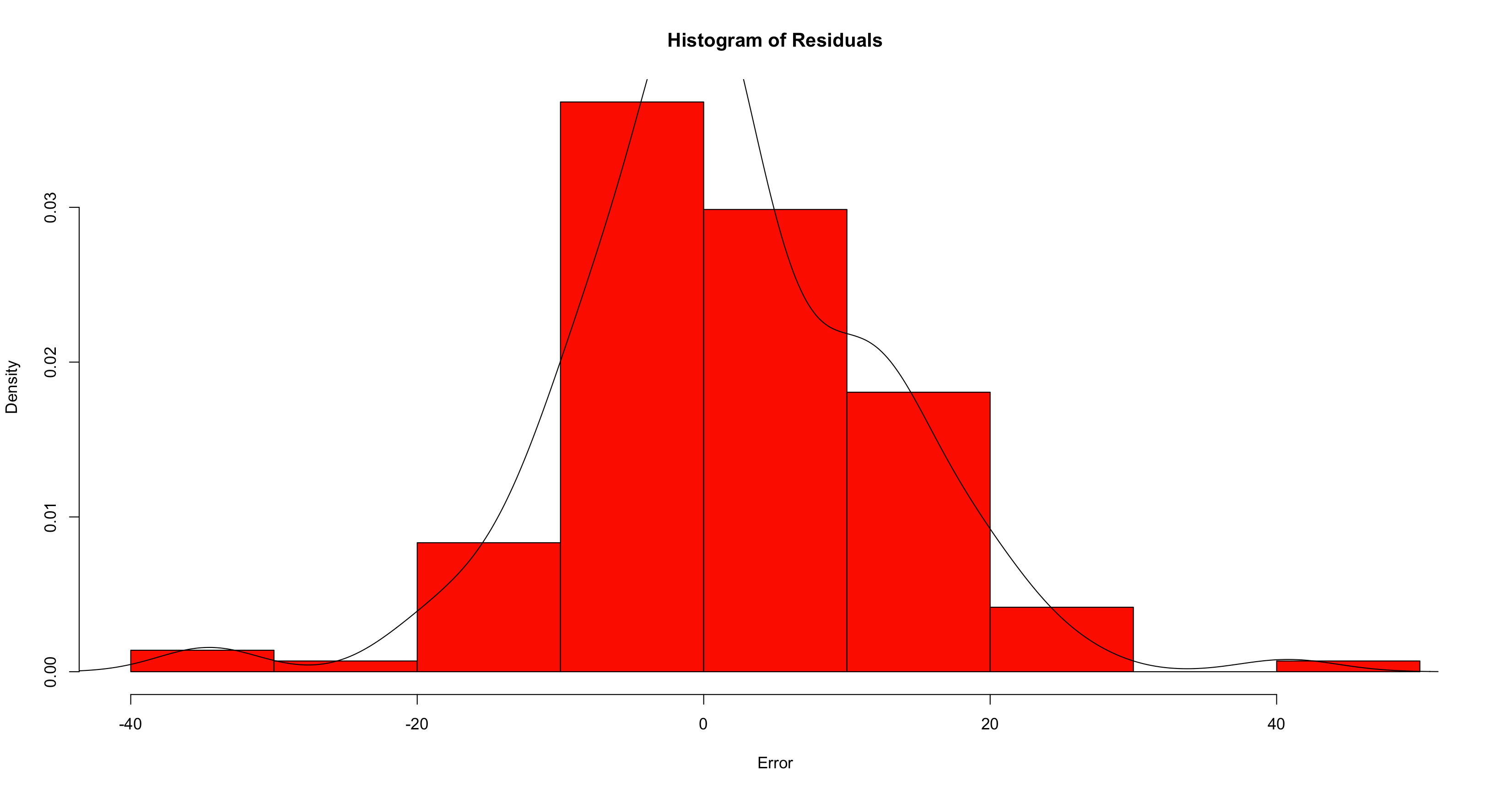

Với đồ thị phân bố (histogram) của phân dư, ta thấy được hầu hết các phần dư đều tập trung xung quanh giá trị 0 và phân phối này khá giống phân phối chuẩn, ta có thể thực hiện một và kiểm định rõ hơn để xác định phân phối chính xác của phần dư này. Tới đây ta có thể nói rằng, không có vấn đề gì với mô hình ARIMA hiện tại.

3.5. Dự báo (Forecast)

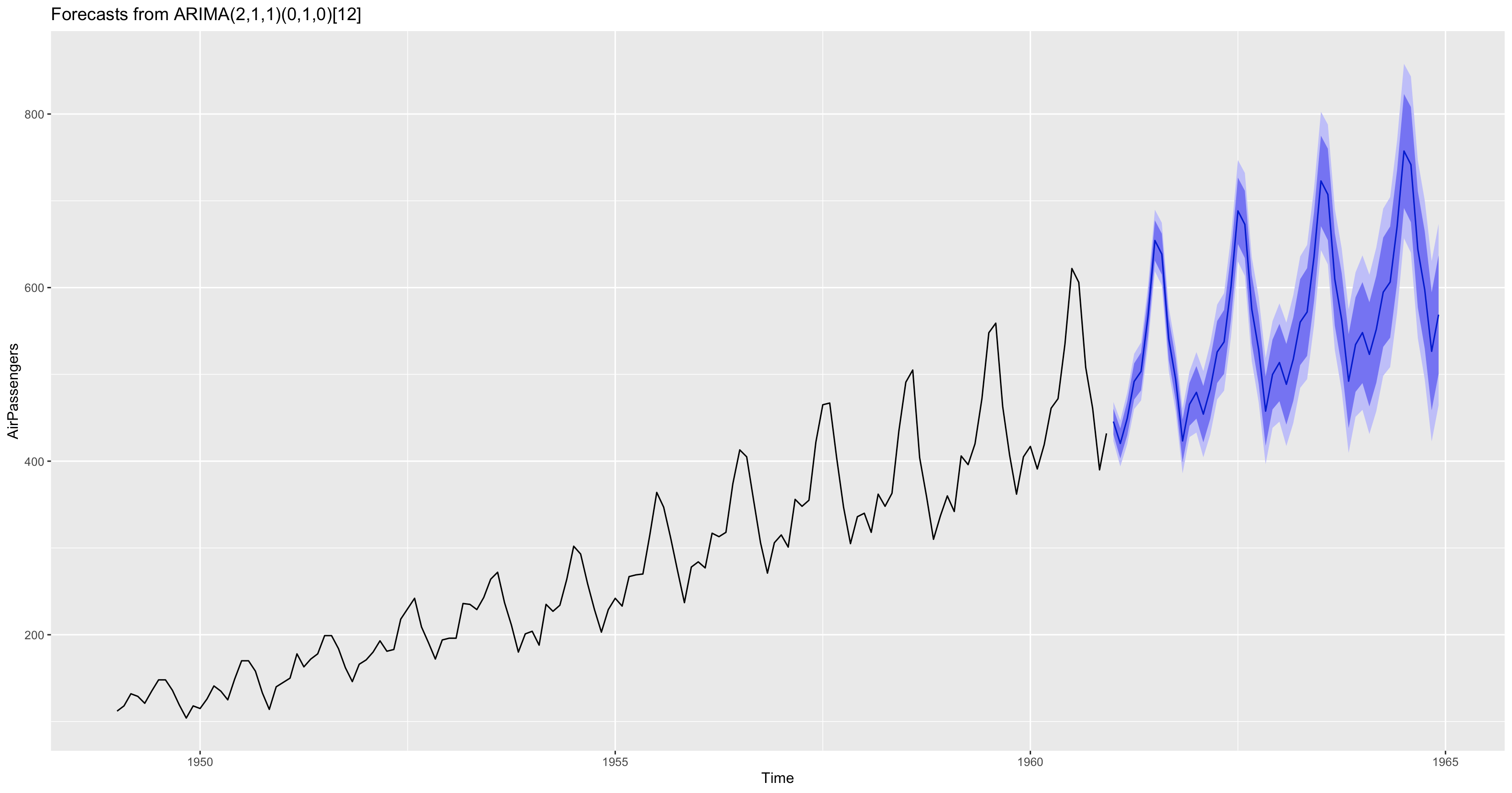
Sử dụng hàm forecast để dự báo cho 48 tháng hay 4 năm tiếp theo trong tương lai. Hai miền màu xanh có trong hình là miền khoảng tin cậy 80% (hẹp) và 95% (rộng) của dự báo.

1f <- forecast(model, 48)
2library(ggplot2)
3autoplot(f)