[Dữ liệu chuỗi thời gian] ĐỒNG TÍCH HỢP VÀ MÔ HÌNH HIỆU CHỈNH SAI SỐ

Trong bài viết này, SciEco cung cấp nội dung về các vấn đề liên quan đến việc ước tính mối quan hệ giữa hai hoặc nhiều chuỗi thời gian không dừng với nghiệm đơn vị và đề cập đến các kỹ thuật kinh tế lượng thích hợp được sử dụng trong phân tích hồi quy với các biến không dừng.

I. HỒI QUY GIẢ VÀ ĐỒNG TÍCH HỢP

1. Hồi quy giả:

Nếu hồi quy giữa các chuỗi thời gian không có tính dừng với nhau cho các kết quả có ý nghĩa thống kê, tuy nhiên lại không có ý nghĩa về bản chất của mối quan hệ kinh tế. Hiện tượng này được gọi là hồi quy giả (spurious regression) hay hồi quy vô nghĩa (non-sense regression).
Dấu hiệu: Khi hồi quy một hoặc nhiều chuỗi không có tính dừng, kết quả hồi quy với các tham số có ý nghĩa thống kê, R^2 trung bình hoặc cao và thống kê Durbin–Watson thấp.
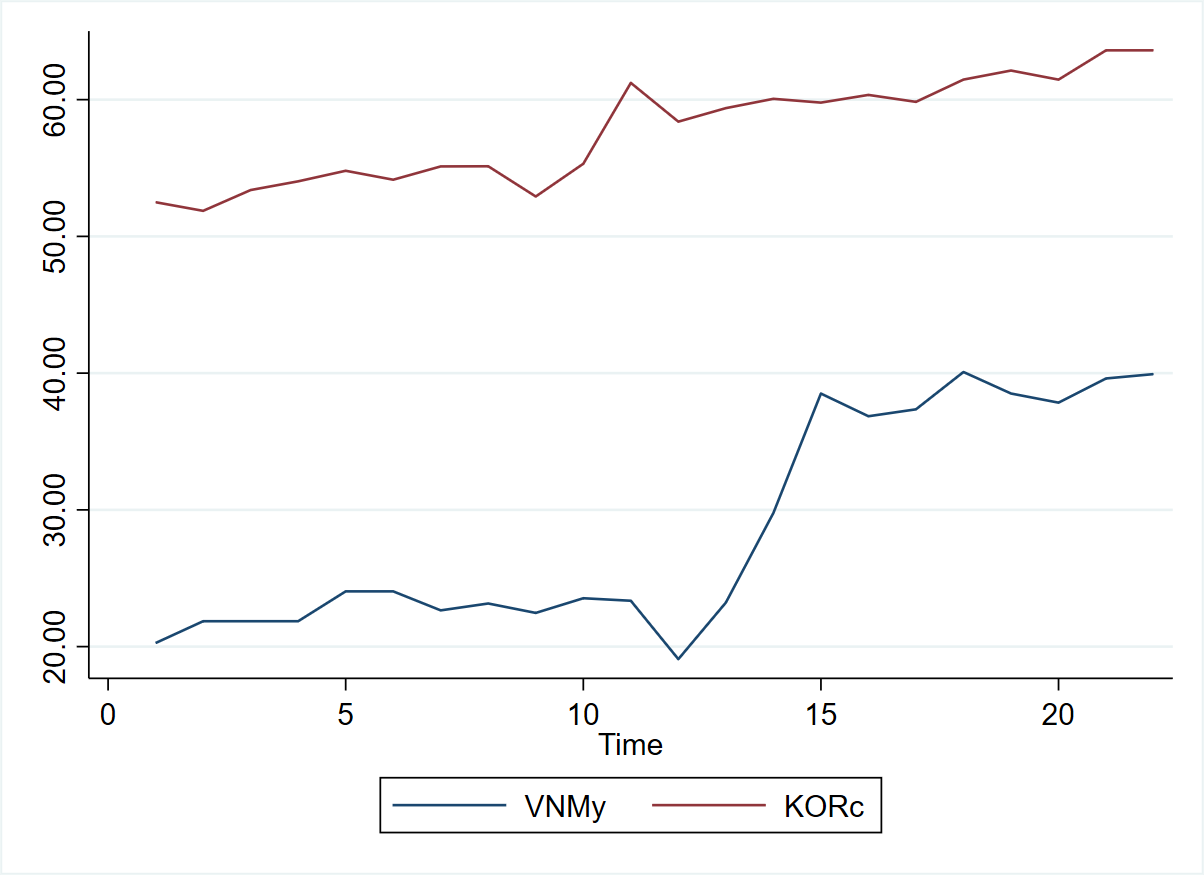
VD: Xem xét hồi quy chuỗi thu nhập của Việt Nam (VNMy) theo tổng chi tiêu của Hàn Quốc (KORc). Dữ liệu từ năm 2000-2021 (WB)

VNMy_t = \beta_0 + \beta_1KORc_t +e_t

Về bản chất, hai biến này không liên quan đến nhau. Tuy nhiên, kết quả hồi quy cho thấy chi tiêu của Hàn Quốc có giải thích rất tốt cho tăng trưởng kinh tế của Việt Nam, thể hiện ở tham số có ý nghĩa thống kê, R^2 =0.73 khá cao, phương trình hồi quy có thống kế F =0.0000 rất nhỏ. Đây là dấu hiệu của hồi quy giả. Nghĩ là: Mô hình hồi quy đẹp với R2 cao, hệ số có dấu đúng như kỳ vọng và có ý nghĩa thống kê dựa trên kiểm định t, nhưng không có ý nghĩa gì về mặt kinh tế.

Để giải quyết vấn đề hồi quy giả hoặc vô nghĩa trong chuỗi thời gian và kiểm tra xem liệu mối quan hệ ngắn hạn và dài hạn có tồn tại giữa các biến không dừng hay không, sử dụng khái niệm đồng tích hợp (cointegration) là một phương pháp phổ biến và hiệu quả.

2. Đồng tích hợp

Một số khái niệm:

Một chuỗi thời gian có thể dừng và không dừng. Trong trường hợp sai phân bậc nhất là một chuỗi dừng thì ta gọi chuỗi tích hợp bậc nhất–chuỗi có nghiệm đơn vị, ký hiệu: I(1). Nếu chuỗi thời gian dừng ở chuỗi gốc– gọi là chuỗi tích hợp bậc 0, ký hiệu: I(0).
Đồng tích hợp (cointergration): Nếu hợp thức tuyến tính của hai hay nhiều chuỗi I(1) cho ta một chuỗi I(0) được gọi là đồng tích hợp. Nghĩa là: khi phần dư trong mô hình hồi quy giữa các chuỗi thời gian không dừng là một chuỗi dừng thì kết quả hồi quy là thực.
Đồng tích hợp hàm ý các chuỗi biến động cùng nhau theo thời gian, vì vậy tồn tạo mối quan hệ trong dài hạn. Các mối quan hệ dài hạn này chặt chẽ với các khái niệm về mối quan hệ cân bằng trong lý thuyết kinh tế và các biến động liên tục của chuỗi thời gian kinh tế trong kinh tế lượng.
Trong kinh tế có nhiều lý thuyết hàm ý tồn tại của một mối quan hệ đồng tích hợp giữa các biến. Ví dụ điển hình: Lý thuyết thu nhập thường xuyên hàm ý mối quan hệ đồng tích hợp giữa thu nhập và tiêu dùng ; lý thuyết tăng trưởng hàm ý giữa thu nhập, tiêu dùng và đầu tư,....

II. PHƯƠNG PHÁP ENGLE-GRANGER VÀ MÔ HÌNH HIỆU CHỈNH SAI SỐ

1. Kiểm định đồng tích hợp: Phương pháp Engle-Granger

Giả sử Y, X1, X2,... Xn là chuỗi I(1), việc kiểm định quan hệ đồng tích hợp giữa biến Y và X1, X2,..,Xn được thể hiện theo các bước dưới đây (còn được gọi là kiểm định Granger-Engel):

Bước 1: Hồi quy biến Y theo X1,X2,....,Xn và lưu phần dư (et) vào 1 biến khác

Y_t=\beta_0+\beta_1X1_t+\beta_2X2_t+.....+e_t

Bước 2: Thực hiện kiểm định nghiệm đơn vị ADF (Augmented Dickey-Fuller) cho chuỗi phần dư et:

\Delta e_t = \beta + \alpha e_{t-1} +\sum^{p} _{i=1} \kappa_i \Delta _{t-i} +u_t

Bước 3: Nếu giả thuyết H0 (có nghiệm đơn vị) bị bác bỏ thì tồn tại đồng tích hợp giữa các biến.

Trong đó: Giá trị của thống kê kiểm định ADF $<$ giá trị tới hạn (theo MacKimnon,2010) $\Rightarrow$ Đủ bác bỏ giả thuyết tồn tại của nghiệm đơn vị hay $e_t \thicksim I(0)$ , có đồng tích hợp giữa các biến.

Lưu ý:

Sử dụng kiểm định ADF không có xu hướng
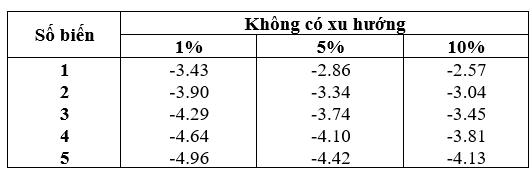
Các giá trị tới hạn của kiểm định nghiệm đơn vị phù hợp cho kiểm định quan hệ đồng tích hợp được xây dựng bởi MacKimnon (2010). Các giá trị này khác nhau theo số biến I(1) của phương trình, được thể hiện ở bảng 1 dưới:

Bảng 1: Các giá trị tới hạn của kiểm định đồng tích hợp (nguồn: MacKimnon, 2010)

2. Mô hình hiệu chỉnh sai số (ECM)

Định lý Granger: Nếu X và Y là đồng tích hợp thì quan hệ giữa chúng được biểu diễn bởi một cơ chế hiệu chỉnh sai số (ECM). Cơ chế này tồn tại khi ít nhất một trong hai biến X, Y phải phản ứng để loại bỏ (một phần) sự mất cân bằng của thời kì trước.

Mô hình ECM đơn giản:

\Delta Y_t = \varphi + \gamma e_{t-1}+\Delta X_t +u_t

Trong đó: $u_t$ là nhiều trắng

Hệ số ECM của $e_{t-1}$ thường được gọi là hệ số hiệu chỉnh (adjustment coefficient). Ý nghĩa của nó là: Y thay đổi nhằm loại bỏ phần mất cân bằng ở thời điểm t-1. Mang dấu âm.

Mô hình ECM tổng quát: gồm có các trễ và có thể có xu thế, có dạng:

\Delta Y_t = \delta + \gamma e_{t-1} +\sum^{p} _{i=1} \phi_i \Delta Y_{t-i} +\sum^{q} _{j=1} \lambda_j \Delta X_{t-j} +u_t

Trong đó, $u_t$ là nhiễu trắng.

Ý nghĩa Mô hình ECM:

Xem xét tác động ngắn hạn thông qua các tham số $\phi_i$ và $\lambda _t$
Hiệu ứng điều chỉnh của Y đối với sự mất cân bằng so với trạng thái dài hạn ở thời kì trước thông qua tham số $\gamma$

Lưu ý: tất cả các biến trong ECM phải là I(0). Vai trò của X và Y ở đây là như nhau.

3. Thực hành với Stata

3.1. Kiểm tra sự đồng liên kết của Engle–Granger

VD: xem xét mối quan hệ giữa chuỗi thu nhập của Việt Nam (VNMy) theo tổng chi tiêu của Hàn Quốc (KORc). Các bước thực hành:

1reg VNMy KORc
2predict e1, resid
3dfuller e1, lag(0)

Kết quả ước tính của OLS được hiển thị theo định dạng sau:

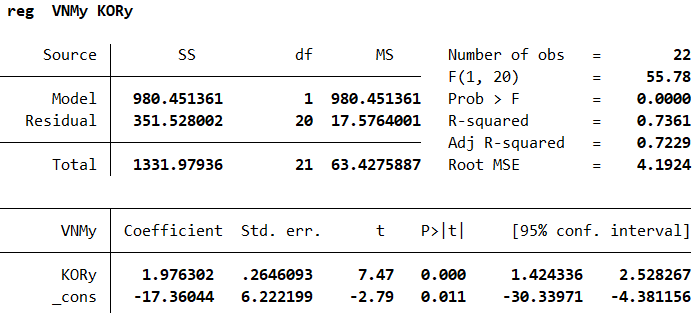
Kiểm định nghiệm đơn vị của phần dư. Thống kê kiểm định ADF(-2.613) > giá trị tới hạn (-3.34 ở mức ý nghĩa 5%) => Không thể bác bỏ giả thuyết H0 về sự tồn tại của nghiệm đơn vị của chuỗi phần dư e.
=> Kết luận không có đồng tích hợp giữa chuỗi thu nhập Việt Nam và tổng chi tiêu của Hàn Quốc trong giai đoạn 2000-2021.

3.2. Mô hình ECM

Ví dụ: giữa hai chuỗi dữ liệu thời gian: tổng chi tiêu của Hàn Quốc (KORc) theo chuỗi thu nhập của Hàn Quốc (KORy)

1reg KORc KORy
2predict e2, resid
3dfuller e2, lag(0)

Phần này lựa chọn độ trễ thích hợp để vừa xem xét được cơ chế hiệu chỉnh vừa phải thỏa mãn điều kiện ut là nhiễu trắng

1reg dl2.KORy
2predict ut, resid
3dfuller ut, lag(0)

Kiểm định nghiệm đơn vị của phần dư e2. Thống kê kiểm định ADF(-3.245) < giá trị tới hạn (-3.04 ở mức ý nghĩa 10%) => e2 là dừng ở mức ý nghĩa 10%.

=> Kết luận có đồng tích hợp hay có mối quan hệ trong dài hạn giữa chuỗi tổng chi tiêu và thu nhập của Hàn Quốc .

=> Hàm ý tồn tại ECM đối với chuỗi KORc hoặc KORy, hoặc của cả 2, nhằm phản ứng lại sự mất cân bằng ở thời kỳ trước đó.

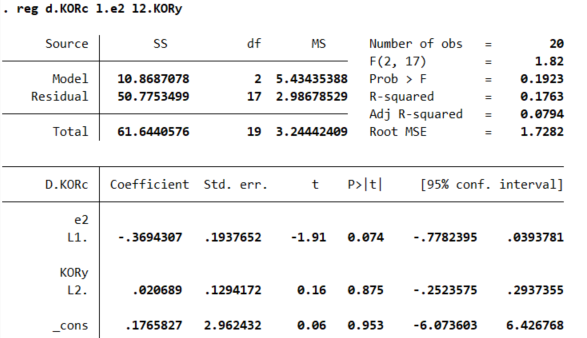
Kết quả cho thấy ECM tồn tại đối với tổng chi tiêu của Hàn Quốc ở mức ý nghĩa 10%. Kết quả này hàm ý, sau mối thời kỳ tổng chi tiêu của Hàn Quốc sẽ điều chỉnh nhằm loại bớt 0.369 phần mất cần bằng ở thời kỳ trước trong mối quan hệ dài hạn giữa tổng chi tiêu với thu nhập của Hàn Quốc.

Nguồn tham khảo:

Panchanan, D. (2019). Econometrics in theory and practice: analysis of cross section, time seriesand panel data with Stata 15.1.
Phạm, Thế Anh. (2022). Giáo trình phân tích định lượng trong kinh tế vĩ mô. Nhà xuất bản Đại học Kinh tế quốc dân.