[Dữ liệu chuỗi thời gian] MÔ HÌNH AR, MA VÀ ARIMA (Phần 2)

2. THỰC HÀNH TRÊN STATA

Trong phần này, chúng ta sẽ sử dụng chỉ số giá tiêu dùng (CPI) của Mỹ từ 1/1/2008 đến 1/2/2021 (tần suất: theo tháng) để tiến hành dự báo với các mô hình được nêu trong bài viết.

2.1. Kiểm định tính dừng của chuỗi số

Trước hết, chúng ta cần kiểm định tính dừng của chuỗi CPI bằng kiểm định ADF như sau:

1dfuller CPI,trend regress

$\rightarrow$ Kết quả kiểm định nghiệm đơn vị được thể hiện theo định dạng sau:

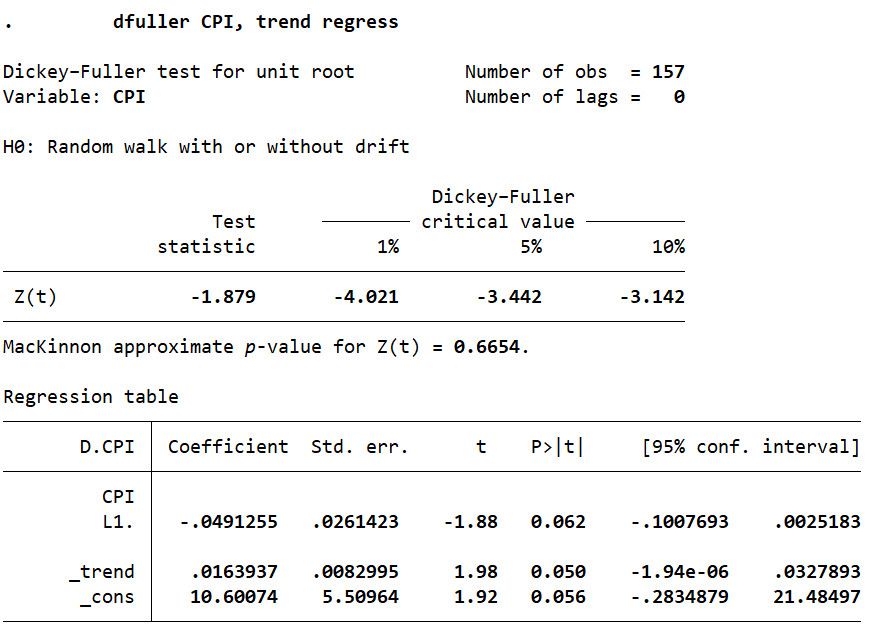
Kết quả cho thấy thống kê kiểm định ADF (-1.879) > giá trị tới hạn (-3.442 ở mức ý nghĩa 5%) $\Rightarrow$ Không thể bác bỏ giá thuyết H0 về sự tồn tại của nghiệm đơn vị của chuỗi CPI $\Rightarrow$ Chuỗi CPI là chuỗi không dừng.

Điều này phản ánh đúng với thực tế rằng đa phần của chuỗi số kinh tế - tài chính đều không dừng tại chuỗi gốc. Do đó, ta sẽ sử dụng sai phân bậc nhất của log chuỗi CPI – hay còn gọi là tốc độ tăng của chỉ số giá tiêu dùng (lạm phát) như sau:

1gen lCPI = ln(CPI)
2gen dlCPI = D.lCPI
3dfuller dlCPI,trend regress

$\rightarrow$ Kết quả kiểm định nghiệm đơn vị được thể hiện theo định dạng sau:

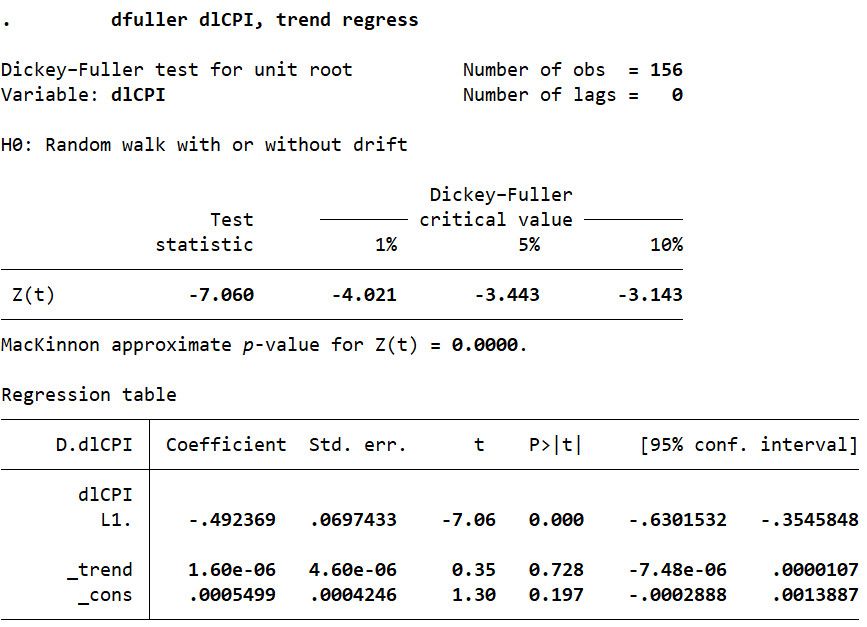
Kết quả cho thấy thống kê kiểm định ADF (-7.060) > giá trị tới hạn (-3.443 ở mức ý nghĩa 5%) $\Rightarrow$ Bác bỏ giá thuyết H0 về sự tồn tại của nghiệm đơn vị của chuỗi dlCPI $\Rightarrow$ Chuỗi dlCPI là chuỗi dừng.

2.2. Lựa chọn độ trễ hợp lý p và q

2.2.1. Lựa chọn độ trễ q*

Để lựa chọn độ trễ q* phù hợp, ta sẽ vẽ hàm tự tương quan (ACF) như sau:

1ac dlCPI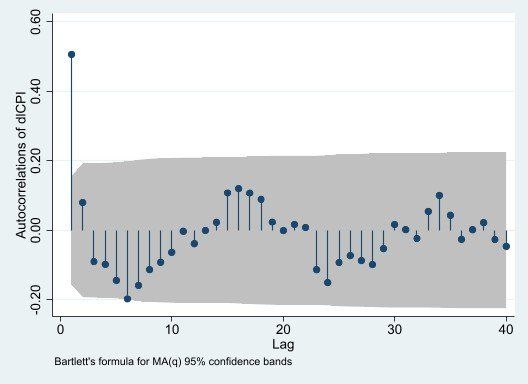

Dựa vào hàm tự tương quan ACF, ta thấy đồ thị ACF đột ngột cắt đứt/bằng 0 kể từ sau độ trễ 1 (về mặt trực quan, kể từ sau độ trễ 1, các giá trị tương quan đều nằm trong khoảng đậm) $\Rightarrow$ q* = 1

2.2.2. Lựa chọn độ trễ p*

Để lựa chọn độ trễ p* phù hợp, ta sẽ vẽ hàm tương quan riêng (PACF) như sau:

1pac dlCPI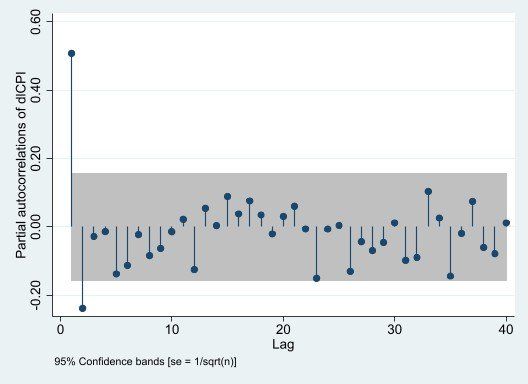

Dựa vào hàm tương quan riêng PACF, ta thấy đồ thị PACF đột ngột cắt đứt/bằng 0 kể từ sau độ trễ 2 (về mặt trực quan, kể từ sau độ trễ 2, các giá trị tương quan riêng đều nằm trong khoảng đậm) $\Rightarrow$ p* = {1,2}.

2.3. Ước lượng, kiểm định và dự báo cho các mô hình

2.3.1. Mô hình AR(1)

Ta sẽ tiến hành ước lượng mô hình AR(1) cho chuỗi dlCPI như sau:

1arima lCPI,arima(1,1,0)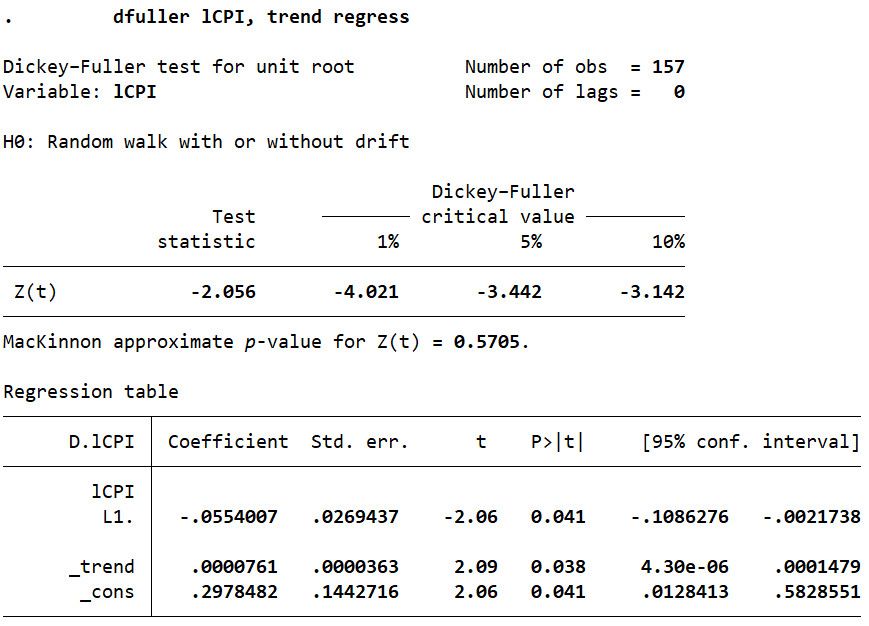

Nhìn chung, ta thấy các hệ số ước lượng đều có ý nghĩa thống kê ở mức ý nghĩa 5%. Tuy nhiên, để có thể sử dụng mô hình này để dự báo, ta cần phải đảm bảo phần dư là nhiễu trắng. Do đó, ta sẽ tiến hành kiểm định phần dư là nhiễu trắng bằng kiểm định Portmanteau như sau:

1arima lCPI,arima(1,1,0)
2predict error1,resid
3wntestq error1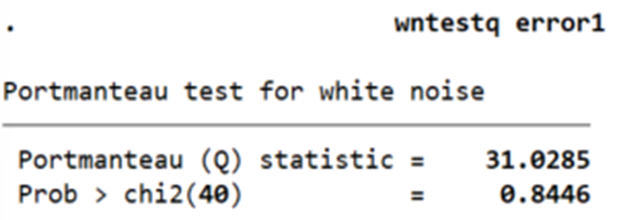

Kết quả kiểm định cho thấy P-value (0.8446) > 0.05 $\Rightarrow$ chưa thể bác bỏ giả thuyết H0 $\Rightarrow$ phần dư trong mô hình AR(1) là nhiễu trắng.

Sau đó, chúng ta sẽ sử dụng mô hình này để dự đoán cho 24 tháng (2 năm) tiếp theo như sau:

1sappend,add(24)
2arima lCPI,arima(1,1,0)
3predict flcpi1,y dynamic(m(2021m3))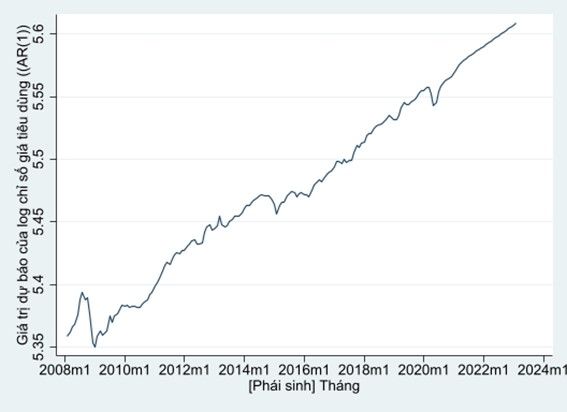

2.3.2. Mô hình MA(1)

Ta sẽ tiến hành ước lượng mô hình MA(1) cho chuỗi dlCPI như sau:

1arima lCPI,arima(0,1,1)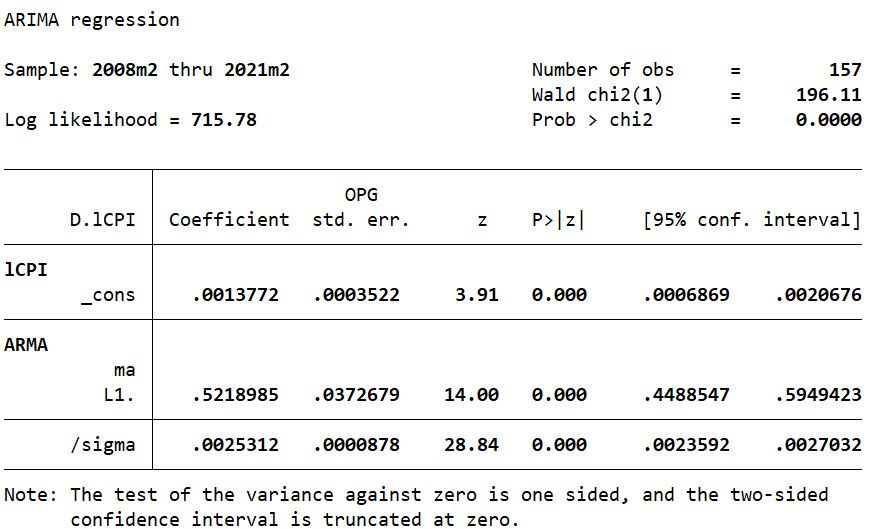

Nhìn chung, ta thấy các hệ số ước lượng đều có ý nghĩa thống kê ở mức ý nghĩa 5%. Tuy nhiên, để có thể sử dụng mô hình này để dự báo, ta cần phải đảm bảo phần dư là nhiễu trắng. Do đó, ta sẽ tiến hành kiểm định phần dư là nhiễu trắng bằng kiểm định Portmanteau như sau:

1arima lCPI,arima(0,1,1)
2predict error2,resid
3wntestq error2

Kết quả kiểm định cho thấy P-value (0.8052) > 0.05 $\Rightarrow$ chưa thể bác bỏ giả thuyết H0 $\Rightarrow$ phần dư trong mô hình MA(1) là nhiễu trắng.

Sau đó, chúng ta sẽ sử dụng mô hình này để dự đoán cho 24 tháng (2 năm) tiếp theo như sau:

1tsappend,add(24) // nếu trước đó đã tạo rồi thì không cần đoạn code này nữa
2arima lCPI,arima(0,1,1)
3predict flcpi2,y dynamic(m(2021m3))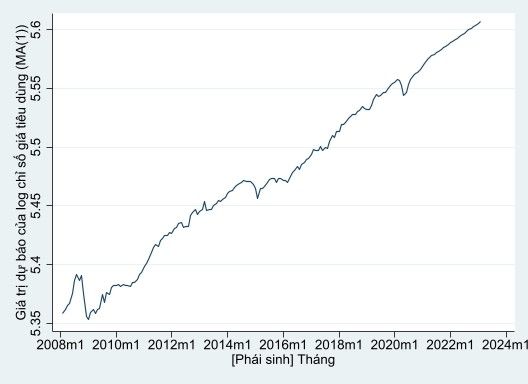

2.3.3. Mô hình ARIMA(1,1,1)

Ta sẽ tiến hành ước lượng mô hình ARIMA(1,1,1) cho chuỗi dlCPI như sau:

1arima lCPI,arima(1,1,1)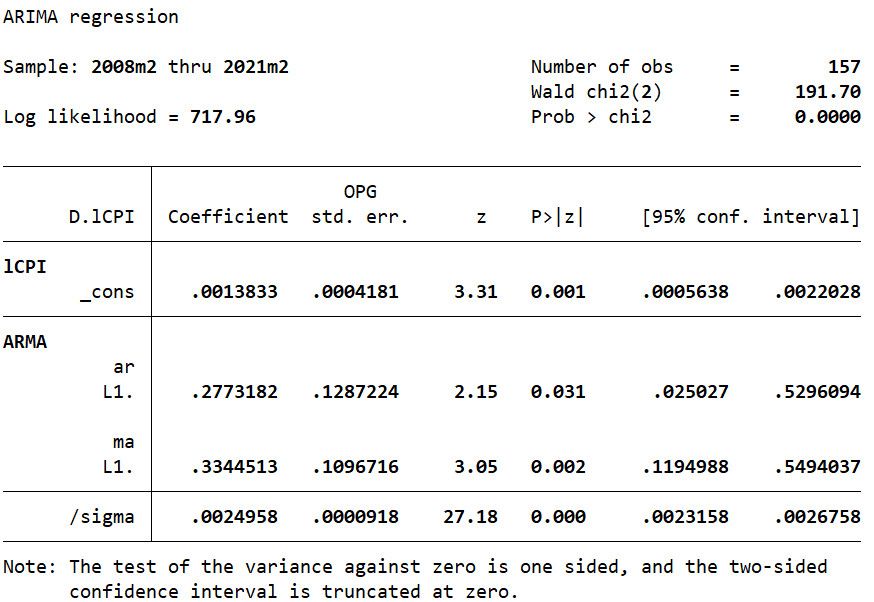

Nhìn chung, ta thấy các hệ số ước lượng đều có ý nghĩa thống kê ở mức ý nghĩa 5%. Tuy nhiên, để có thể sử dụng mô hình này để dự báo, ta cần phải đảm bảo phần dư là nhiễu trắng. Do đó, ta sẽ tiến hành kiểm định phần dư là nhiễu trắng bằng kiểm định Portmanteau như sau:

1arima lCPI,arima(1,1,1)
2predict error3,resid
3wntestq error3

Kết quả kiểm định cho thấy P-value (0.9727) > 0.05 $\Rightarrow$ chưa thể bác bỏ giả thuyết H0 $\Rightarrow$ phần dư trong mô hình ARIMA(1,1,1) là nhiễu trắng.

Sau đó, chúng ta sẽ sử dụng mô hình này để dự đoán cho 24 tháng (2 năm) tiếp theo như sau:

1tsappend,add(24) // nếu trước đó đã tạo rồi thì không cần đoạn code này nữa
2arima lCPI,arima(1,1,1)
3predict flcpi3,y dynamic(m(2021m3))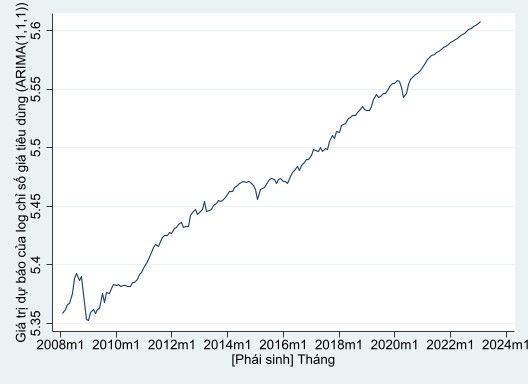

Nguồn tham khảo:

1. Phạm, Thế Anh. (2022). Giáo trình phân tích định lượng trong kinh tế vĩ mô. Nhà xuất bản Đại học Kinh tế quốc dân.